How to iron out rough landscapes and get optimal performances: Replicated Gradient Descent and its application to tensor PCA

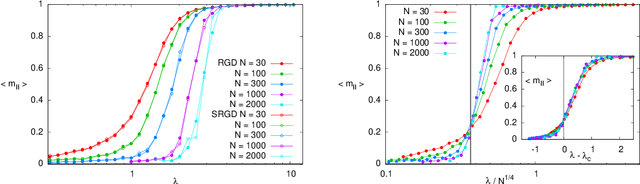
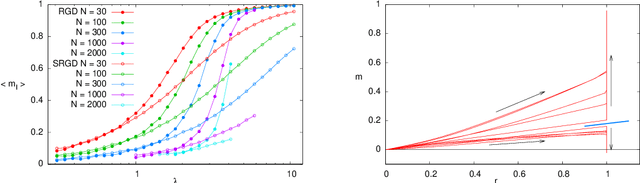
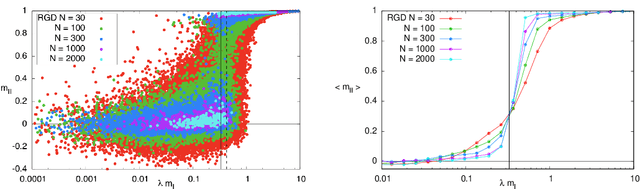
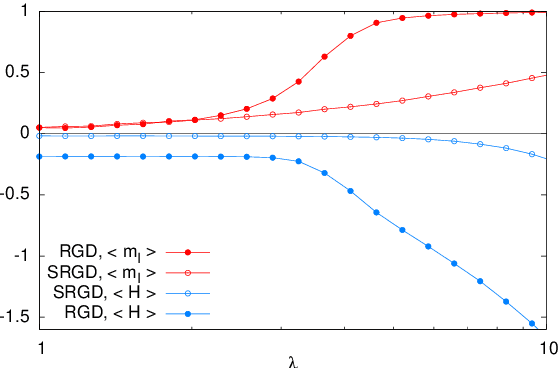
In many high-dimensional estimation problems the main task consists in minimizing a cost function, which is often strongly non-convex when scanned in the space of parameters to be estimated. A standard solution to flatten the corresponding rough landscape consists in summing the losses associated to different data points and obtain a smoother empirical risk. Here we propose a complementary method that works for a single data point. The main idea is that a large amount of the roughness is uncorrelated in different parts of the landscape. One can then substantially reduce the noise by evaluating an empirical average of the gradient obtained as a sum over many random independent positions in the space of parameters to be optimized. We present an algorithm, called Replicated Gradient Descent, based on this idea and we apply it to tensor PCA, which is a very hard estimation problem. We show that Replicated Gradient Descent over-performs physical algorithms such as gradient descent and approximate message passing and matches the best algorithmic thresholds known so far, obtained by tensor unfolding and methods based on sum-of-squares.