Learning by message-passing in networks of discrete synapses
Paper and Code
Dec 09, 2005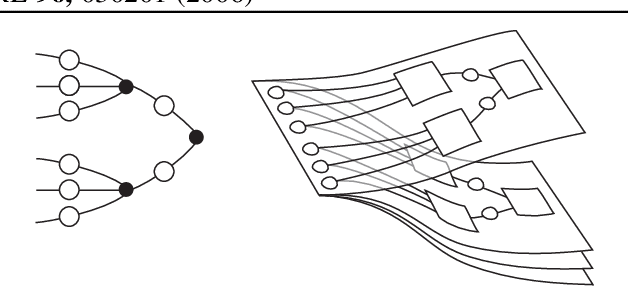
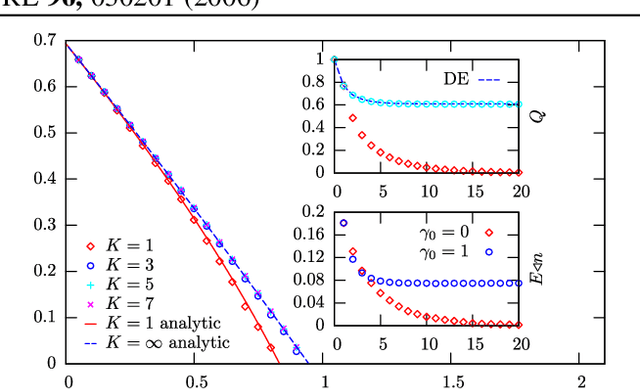
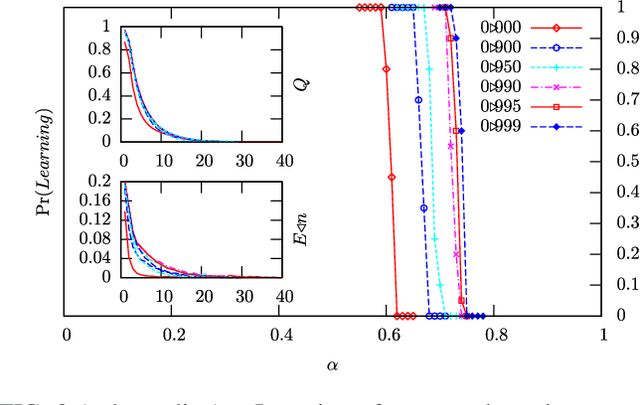
We show that a message-passing process allows to store in binary "material" synapses a number of random patterns which almost saturates the information theoretic bounds. We apply the learning algorithm to networks characterized by a wide range of different connection topologies and of size comparable with that of biological systems (e.g. $n\simeq10^{5}-10^{6}$). The algorithm can be turned into an on-line --fault tolerant-- learning protocol of potential interest in modeling aspects of synaptic plasticity and in building neuromorphic devices.
* Phys. Rev. Lett. 96, 030201 (2006) * 4 pages, 3 figures; references updated and minor corrections;
accepted in PRL
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge