Regularization of Mixture Models for Robust Principal Graph Learning

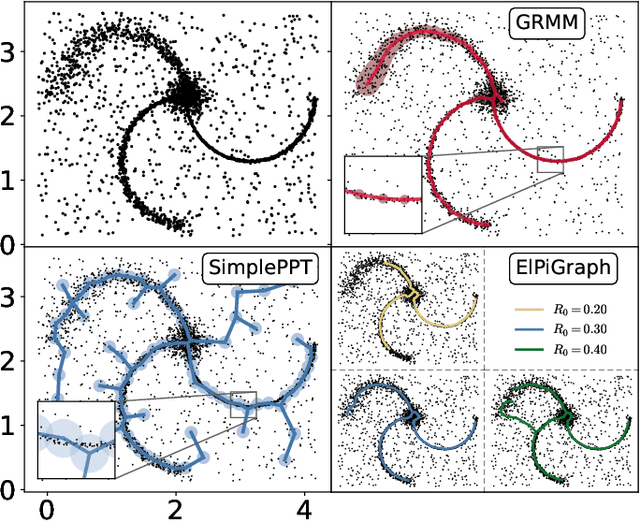
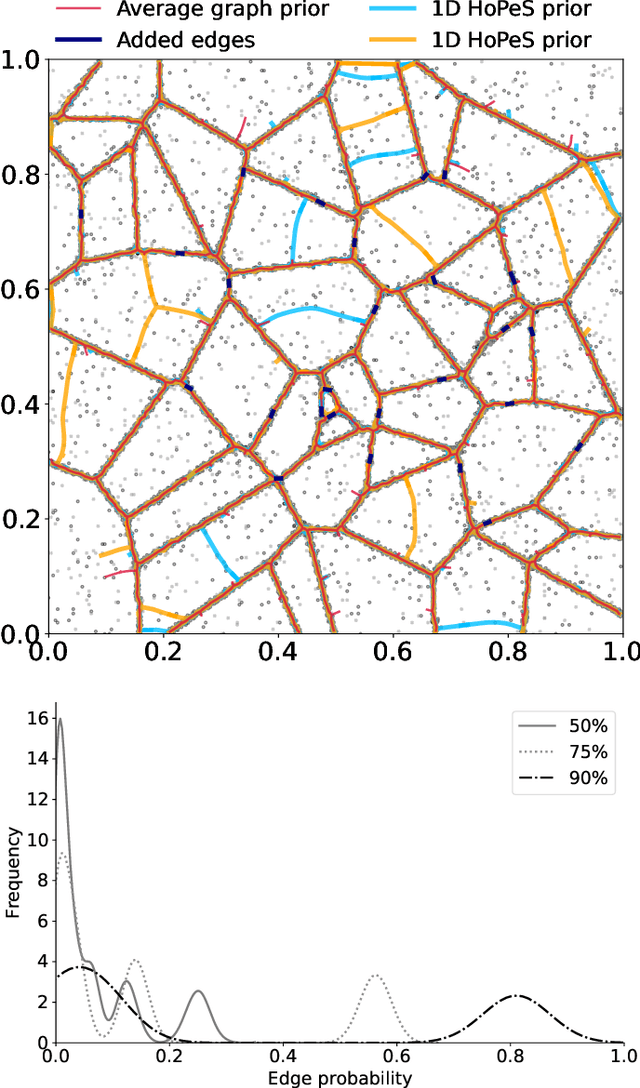
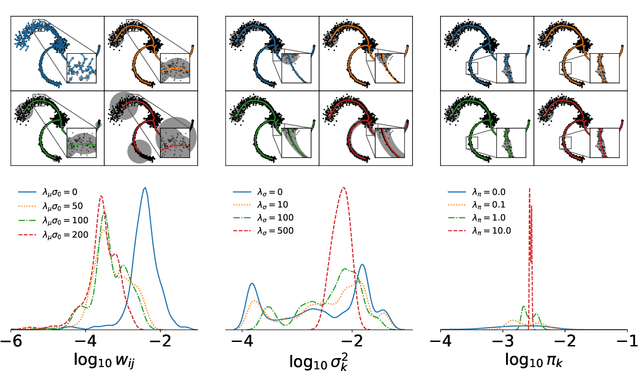
A regularized version of Mixture Models is proposed to learn a principal graph from a distribution of $D$-dimensional data points. In the particular case of manifold learning for ridge detection, we assume that the underlying manifold can be modeled as a graph structure acting like a topological prior for the Gaussian clusters turning the problem into a maximum a posteriori estimation. Parameters of the model are iteratively estimated through an Expectation-Maximization procedure making the learning of the structure computationally efficient with guaranteed convergence for any graph prior in a polynomial time. We also embed in the formalism a natural way to make the algorithm robust to outliers of the pattern and heteroscedasticity of the manifold sampling coherently with the graph structure. The method uses a graph prior given by the minimum spanning tree that we extend using random sub-samplings of the dataset to take into account cycles that can be observed in the spatial distribution.

Encoding large scale cosmological structure with Generative Adversarial Networks

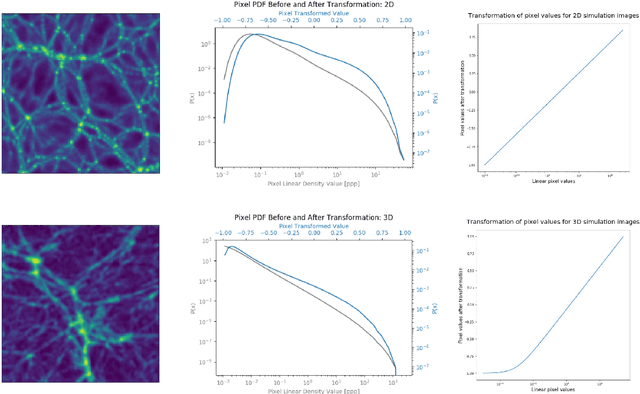
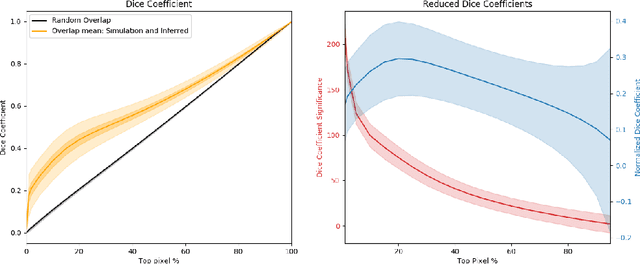
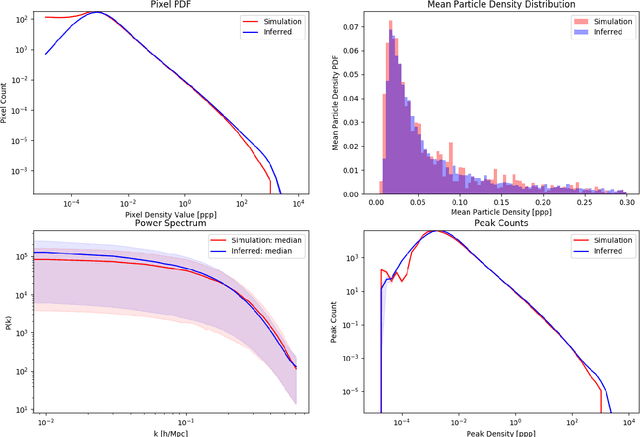
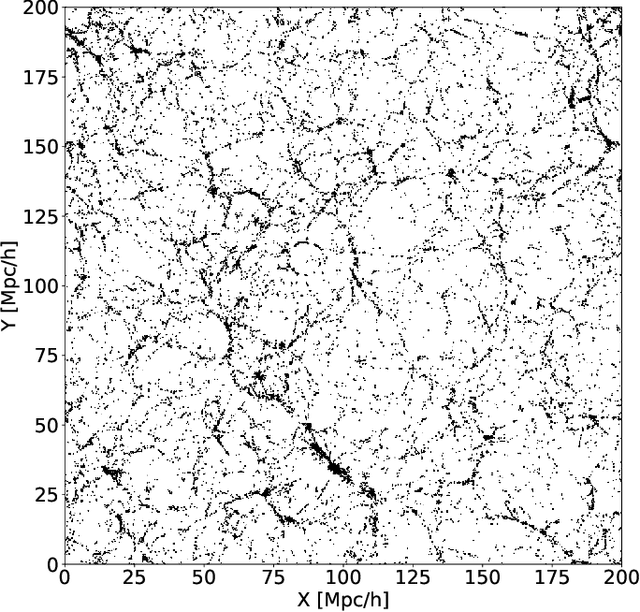
Recently a type of neural networks called Generative Adversarial Networks (GANs) has been proposed as a solution for fast generation of simulation-like datasets, in an attempt to bypass heavy computations and expensive cosmological simulations to run in terms of time and computing power. In the present work, we build and train a GAN to look further into the strengths and limitations of such an approach. We then propose a novel method in which we make use of a trained GAN to construct a simple autoencoder (AE) as a first step towards building a predictive model. Both the GAN and AE are trained on images issued from two types of N-body simulations, namely 2D and 3D simulations. We find that the GAN successfully generates new images that are statistically consistent with the images it was trained on. We then show that the AE manages to efficiently extract information from simulation images, satisfyingly inferring the latent encoding of the GAN to generate an image with similar large scale structures.