Unbalancedness in Neural Monge Maps Improves Unpaired Domain Translation

In optimal transport (OT), a Monge map is known as a mapping that transports a source distribution to a target distribution in the most cost-efficient way. Recently, multiple neural estimators for Monge maps have been developed and applied in diverse unpaired domain translation tasks, e.g. in single-cell biology and computer vision. However, the classic OT framework enforces mass conservation, which makes it prone to outliers and limits its applicability in real-world scenarios. The latter can be particularly harmful in OT domain translation tasks, where the relative position of a sample within a distribution is explicitly taken into account. While unbalanced OT tackles this challenge in the discrete setting, its integration into neural Monge map estimators has received limited attention. We propose a theoretically grounded method to incorporate unbalancedness into any Monge map estimator. We improve existing estimators to model cell trajectories over time and to predict cellular responses to perturbations. Moreover, our approach seamlessly integrates with the OT flow matching (OT-FM) framework. While we show that OT-FM performs competitively in image translation, we further improve performance by incorporating unbalancedness (UOT-FM), which better preserves relevant features. We hence establish UOT-FM as a principled method for unpaired image translation.

Unbalanced Low-rank Optimal Transport Solvers

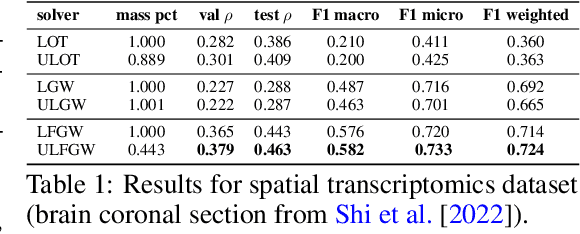
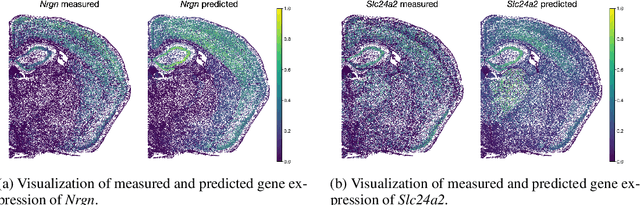
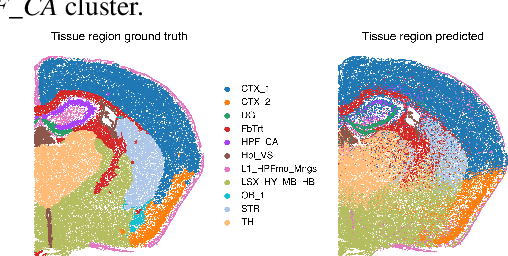
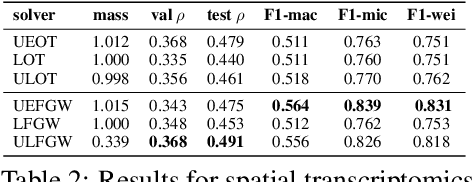
The relevance of optimal transport methods to machine learning has long been hindered by two salient limitations. First, the $O(n^3)$ computational cost of standard sample-based solvers (when used on batches of $n$ samples) is prohibitive. Second, the mass conservation constraint makes OT solvers too rigid in practice: because they must match \textit{all} points from both measures, their output can be heavily influenced by outliers. A flurry of recent works in OT has addressed these computational and modelling limitations, but has resulted in two separate strains of methods: While the computational outlook was much improved by entropic regularization, more recent $O(n)$ linear-time \textit{low-rank} solvers hold the promise to scale up OT further. On the other hand, modelling rigidities have been eased owing to unbalanced variants of OT, that rely on penalization terms to promote, rather than impose, mass conservation. The goal of this paper is to merge these two strains, to achieve the promise of \textit{both} versatile/scalable unbalanced/low-rank OT solvers. We propose custom algorithms to implement these extensions for the linear OT problem and its Fused-Gromov-Wasserstein generalization, and demonstrate their practical relevance to challenging spatial transcriptomics matching problems.

Uncertainty Quantification for Atlas-Level Cell Type Transfer

Single-cell reference atlases are large-scale, cell-level maps that capture cellular heterogeneity within an organ using single cell genomics. Given their size and cellular diversity, these atlases serve as high-quality training data for the transfer of cell type labels to new datasets. Such label transfer, however, must be robust to domain shifts in gene expression due to measurement technique, lab specifics and more general batch effects. This requires methods that provide uncertainty estimates on the cell type predictions to ensure correct interpretation. Here, for the first time, we introduce uncertainty quantification methods for cell type classification on single-cell reference atlases. We benchmark four model classes and show that currently used models lack calibration, robustness, and actionable uncertainty scores. Furthermore, we demonstrate how models that quantify uncertainty are better suited to detect unseen cell types in the setting of atlas-level cell type transfer.