Unbalanced Low-rank Optimal Transport Solvers
Paper and Code
May 31, 2023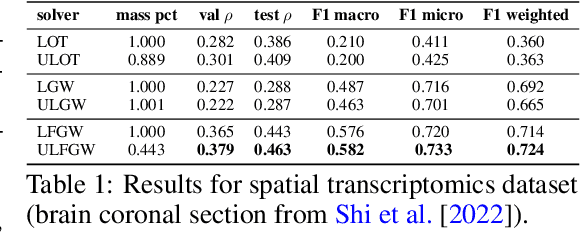
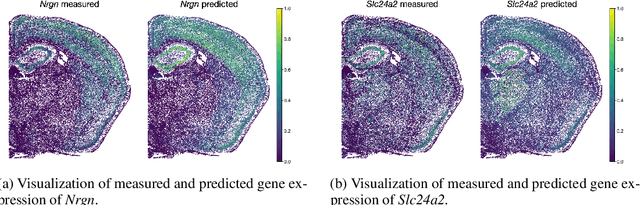
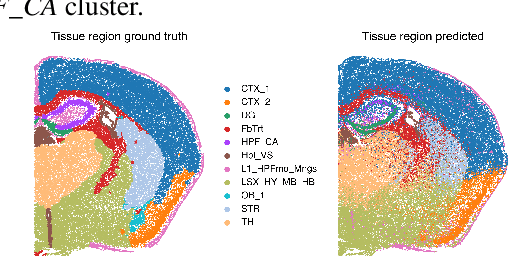
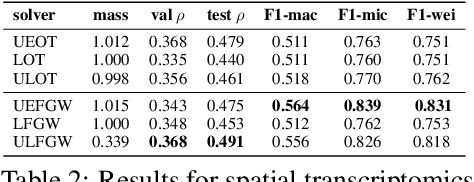
The relevance of optimal transport methods to machine learning has long been hindered by two salient limitations. First, the $O(n^3)$ computational cost of standard sample-based solvers (when used on batches of $n$ samples) is prohibitive. Second, the mass conservation constraint makes OT solvers too rigid in practice: because they must match \textit{all} points from both measures, their output can be heavily influenced by outliers. A flurry of recent works in OT has addressed these computational and modelling limitations, but has resulted in two separate strains of methods: While the computational outlook was much improved by entropic regularization, more recent $O(n)$ linear-time \textit{low-rank} solvers hold the promise to scale up OT further. On the other hand, modelling rigidities have been eased owing to unbalanced variants of OT, that rely on penalization terms to promote, rather than impose, mass conservation. The goal of this paper is to merge these two strains, to achieve the promise of \textit{both} versatile/scalable unbalanced/low-rank OT solvers. We propose custom algorithms to implement these extensions for the linear OT problem and its Fused-Gromov-Wasserstein generalization, and demonstrate their practical relevance to challenging spatial transcriptomics matching problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge