Unbalancedness in Neural Monge Maps Improves Unpaired Domain Translation

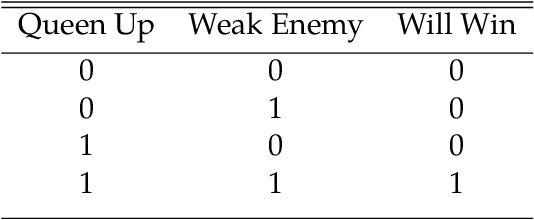
In optimal transport (OT), a Monge map is known as a mapping that transports a source distribution to a target distribution in the most cost-efficient way. Recently, multiple neural estimators for Monge maps have been developed and applied in diverse unpaired domain translation tasks, e.g. in single-cell biology and computer vision. However, the classic OT framework enforces mass conservation, which makes it prone to outliers and limits its applicability in real-world scenarios. The latter can be particularly harmful in OT domain translation tasks, where the relative position of a sample within a distribution is explicitly taken into account. While unbalanced OT tackles this challenge in the discrete setting, its integration into neural Monge map estimators has received limited attention. We propose a theoretically grounded method to incorporate unbalancedness into any Monge map estimator. We improve existing estimators to model cell trajectories over time and to predict cellular responses to perturbations. Moreover, our approach seamlessly integrates with the OT flow matching (OT-FM) framework. While we show that OT-FM performs competitively in image translation, we further improve performance by incorporating unbalancedness (UOT-FM), which better preserves relevant features. We hence establish UOT-FM as a principled method for unpaired image translation.

Generative Entropic Neural Optimal Transport To Map Within and Across Spaces

Learning measure-to-measure mappings is a crucial task in machine learning, featured prominently in generative modeling. Recent years have witnessed a surge of techniques that draw inspiration from optimal transport (OT) theory. Combined with neural network models, these methods collectively known as \textit{Neural OT} use optimal transport as an inductive bias: such mappings should be optimal w.r.t. a given cost function, in the sense that they are able to move points in a thrifty way, within (by minimizing displacements) or across spaces (by being isometric). This principle, while intuitive, is often confronted with several practical challenges that require adapting the OT toolbox: cost functions other than the squared-Euclidean cost can be challenging to handle, the deterministic formulation of Monge maps leaves little flexibility, mapping across incomparable spaces raises multiple challenges, while the mass conservation constraint inherent to OT can provide too much credit to outliers. While each of these mismatches between practice and theory has been addressed independently in various works, we propose in this work an elegant framework to unify them, called \textit{generative entropic neural optimal transport} (GENOT). GENOT can accommodate any cost function; handles randomness using conditional generative models; can map points across incomparable spaces, and can be used as an \textit{unbalanced} solver. We evaluate our approach through experiments conducted on various synthetic datasets and demonstrate its practicality in single-cell biology. In this domain, GENOT proves to be valuable for tasks such as modeling cell development, predicting cellular responses to drugs, and translating between different data modalities of cells.

Neural Networks for Chess

AlphaZero, Leela Chess Zero and Stockfish NNUE revolutionized Computer Chess. This book gives a complete introduction into the technical inner workings of such engines. The book is split into four main chapters -- excluding chapter 1 (introduction) and chapter 6 (conclusion): Chapter 2 introduces neural networks and covers all the basic building blocks that are used to build deep networks such as those used by AlphaZero. Contents include the perceptron, back-propagation and gradient descent, classification, regression, multilayer perceptron, vectorization techniques, convolutional networks, squeeze and excitation networks, fully connected networks, batch normalization and rectified linear units, residual layers, overfitting and underfitting. Chapter 3 introduces classical search techniques used for chess engines as well as those used by AlphaZero. Contents include minimax, alpha-beta search, and Monte Carlo tree search. Chapter 4 shows how modern chess engines are designed. Aside from the ground-breaking AlphaGo, AlphaGo Zero and AlphaZero we cover Leela Chess Zero, Fat Fritz, Fat Fritz 2 and Efficiently Updatable Neural Networks (NNUE) as well as Maia. Chapter 5 is about implementing a miniaturized AlphaZero. Hexapawn, a minimalistic version of chess, is used as an example for that. Hexapawn is solved by minimax search and training positions for supervised learning are generated. Then as a comparison, an AlphaZero-like training loop is implemented where training is done via self-play combined with reinforcement learning. Finally, AlphaZero-like training and supervised training are compared.

Polyconvex anisotropic hyperelasticity with neural networks

In the present work, two machine learning based constitutive models for finite deformations are proposed. Using input convex neural networks, the models are hyperelastic, anisotropic and fulfill the polyconvexity condition, which implies ellipticity and thus ensures material stability. The first constitutive model is based on a set of polyconvex, anisotropic and objective invariants. The second approach is formulated in terms of the deformation gradient, its cofactor and determinant, uses group symmetrization to fulfill the material symmetry condition, and data augmentation to fulfill objectivity approximately. The extension of the dataset for the data augmentation approach is based on mechanical considerations and does not require additional experimental or simulation data. The models are calibrated with highly challenging simulation data of cubic lattice metamaterials, including finite deformations and lattice instabilities. A moderate amount of calibration data is used, based on deformations which are commonly applied in experimental investigations. While the invariant-based model shows drawbacks for several deformation modes, the model based on the deformation gradient alone is able to reproduce and predict the effective material behavior very well and exhibits excellent generalization capabilities. Thus, in particular the second model presents a highly flexible constitutive modeling approach, that leads to a mathematically well-posed problem.

The Stroke Correspondence Problem, Revisited

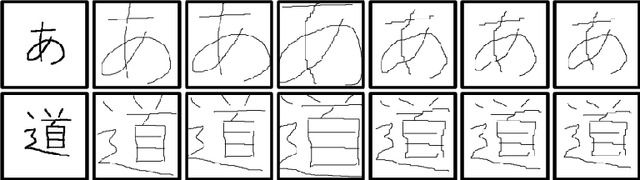
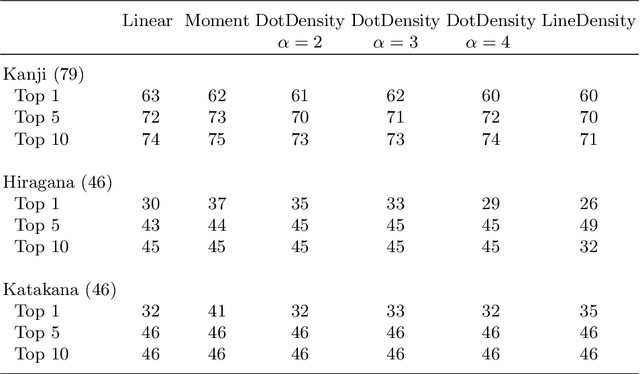
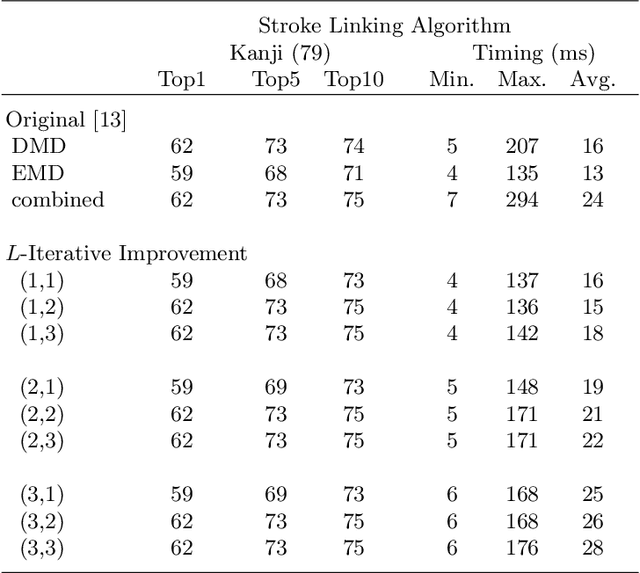
We revisit the stroke correspondence problem [13,14]. We optimize this algorithm by 1) evaluating suitable preprocessing (normalization) methods 2) extending the algorithm with an additional distance measure to handle Hiragana, Katakana and Kanji characters with a low number of strokes and c) simplify the stroke linking algorithms. Our contributions are implemented in the free, open-source library ctegaki and in the demo-tools jTegaki and Kanjicanvas.