Stable Port-Hamiltonian Neural Networks

In recent years, nonlinear dynamic system identification using artificial neural networks has garnered attention due to its manifold potential applications in virtually all branches of science and engineering. However, purely data-driven approaches often struggle with extrapolation and may yield physically implausible forecasts. Furthermore, the learned dynamics can exhibit instabilities, making it difficult to apply such models safely and robustly. This article proposes stable port-Hamiltonian neural networks, a machine learning architecture that incorporates the physical biases of energy conservation or dissipation while guaranteeing global Lyapunov stability of the learned dynamics. Evaluations with illustrative examples and real-world measurement data demonstrate the model's ability to generalize from sparse data, outperforming purely data-driven approaches and avoiding instability issues. In addition, the model's potential for data-driven surrogate modeling is highlighted in application to multi-physics simulation data.

Machine Learning with Physics Knowledge for Prediction: A Survey

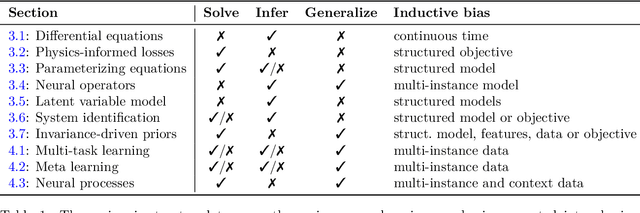
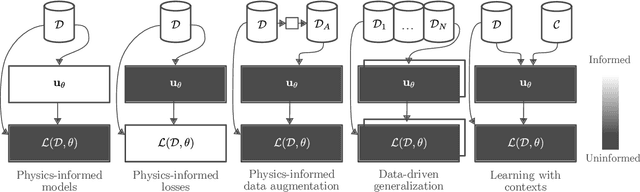
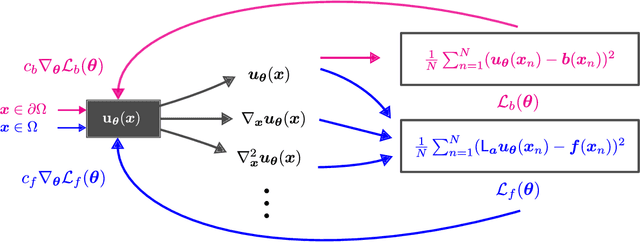
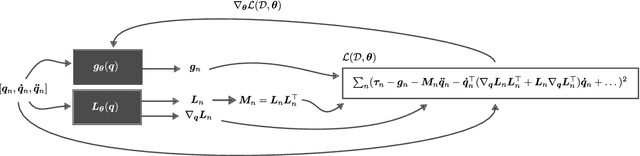
This survey examines the broad suite of methods and models for combining machine learning with physics knowledge for prediction and forecast, with a focus on partial differential equations. These methods have attracted significant interest due to their potential impact on advancing scientific research and industrial practices by improving predictive models with small- or large-scale datasets and expressive predictive models with useful inductive biases. The survey has two parts. The first considers incorporating physics knowledge on an architectural level through objective functions, structured predictive models, and data augmentation. The second considers data as physics knowledge, which motivates looking at multi-task, meta, and contextual learning as an alternative approach to incorporating physics knowledge in a data-driven fashion. Finally, we also provide an industrial perspective on the application of these methods and a survey of the open-source ecosystem for physics-informed machine learning.

TwinLab: a framework for data-efficient training of non-intrusive reduced-order models for digital twins

Purpose: Simulation-based digital twins represent an effort to provide high-accuracy real-time insights into operational physical processes. However, the computation time of many multi-physical simulation models is far from real-time. It might even exceed sensible time frames to produce sufficient data for training data-driven reduced-order models. This study presents TwinLab, a framework for data-efficient, yet accurate training of neural-ODE type reduced-order models with only two data sets. Design/methodology/approach: Correlations between test errors of reduced-order models and distinct features of corresponding training data are investigated. Having found the single best data sets for training, a second data set is sought with the help of similarity and error measures to enrich the training process effectively. Findings: Adding a suitable second training data set in the training process reduces the test error by up to 49% compared to the best base reduced-order model trained only with one data set. Such a second training data set should at least yield a good reduced-order model on its own and exhibit higher levels of dissimilarity to the base training data set regarding the respective excitation signal. Moreover, the base reduced-order model should have elevated test errors on the second data set. The relative error of the time series ranges from 0.18% to 0.49%. Prediction speed-ups of up to a factor of 36,000 are observed. Originality: The proposed computational framework facilitates the automated, data-efficient extraction of non-intrusive reduced-order models for digital twins from existing simulation models, independent of the simulation software.

Polyconvex anisotropic hyperelasticity with neural networks

In the present work, two machine learning based constitutive models for finite deformations are proposed. Using input convex neural networks, the models are hyperelastic, anisotropic and fulfill the polyconvexity condition, which implies ellipticity and thus ensures material stability. The first constitutive model is based on a set of polyconvex, anisotropic and objective invariants. The second approach is formulated in terms of the deformation gradient, its cofactor and determinant, uses group symmetrization to fulfill the material symmetry condition, and data augmentation to fulfill objectivity approximately. The extension of the dataset for the data augmentation approach is based on mechanical considerations and does not require additional experimental or simulation data. The models are calibrated with highly challenging simulation data of cubic lattice metamaterials, including finite deformations and lattice instabilities. A moderate amount of calibration data is used, based on deformations which are commonly applied in experimental investigations. While the invariant-based model shows drawbacks for several deformation modes, the model based on the deformation gradient alone is able to reproduce and predict the effective material behavior very well and exhibits excellent generalization capabilities. Thus, in particular the second model presents a highly flexible constitutive modeling approach, that leads to a mathematically well-posed problem.