Machine Learning with Physics Knowledge for Prediction: A Survey

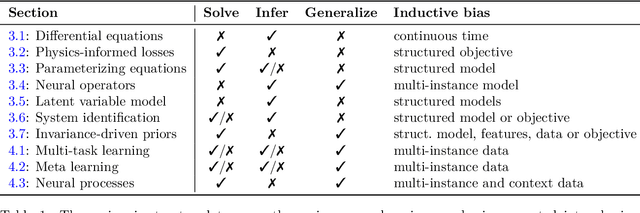
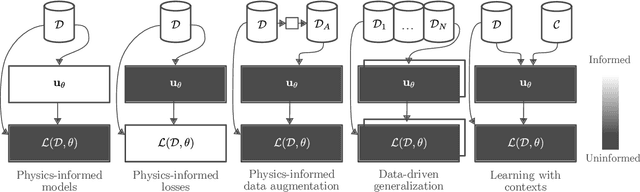
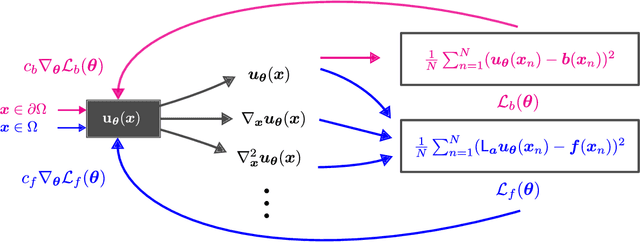
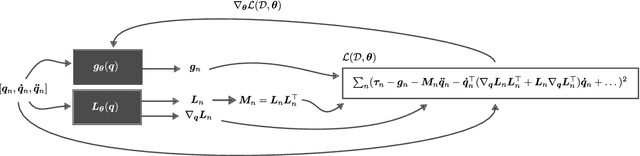
This survey examines the broad suite of methods and models for combining machine learning with physics knowledge for prediction and forecast, with a focus on partial differential equations. These methods have attracted significant interest due to their potential impact on advancing scientific research and industrial practices by improving predictive models with small- or large-scale datasets and expressive predictive models with useful inductive biases. The survey has two parts. The first considers incorporating physics knowledge on an architectural level through objective functions, structured predictive models, and data augmentation. The second considers data as physics knowledge, which motivates looking at multi-task, meta, and contextual learning as an alternative approach to incorporating physics knowledge in a data-driven fashion. Finally, we also provide an industrial perspective on the application of these methods and a survey of the open-source ecosystem for physics-informed machine learning.

Probing optimisation in physics-informed neural networks

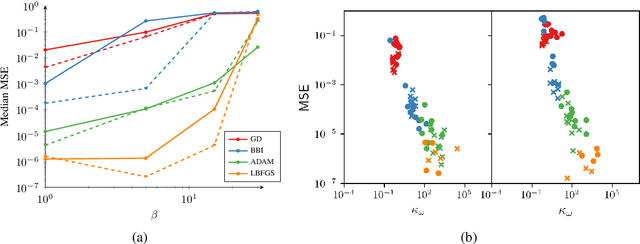
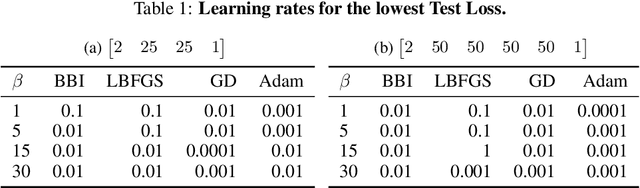
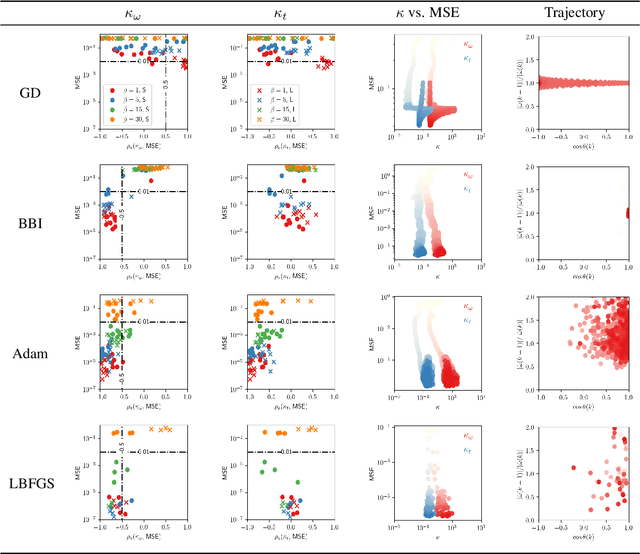
A novel comparison is presented of the effect of optimiser choice on the accuracy of physics-informed neural networks (PINNs). To give insight into why some optimisers are better, a new approach is proposed that tracks the training trajectory curvature and can be evaluated on the fly at a low computational cost. The linear advection equation is studied for several advective velocities, and we show that the optimiser choice substantially impacts PINNs model performance and accuracy. Furthermore, using the curvature measure, we found a negative correlation between the convergence error and the curvature in the optimiser local reference frame. It is concluded that, in this case, larger local curvature values result in better solutions. Consequently, optimisation of PINNs is made more difficult as minima are in highly curved regions.