Probing optimisation in physics-informed neural networks

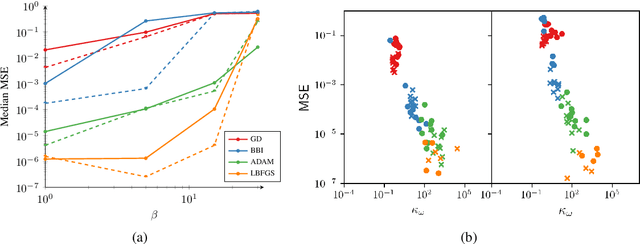
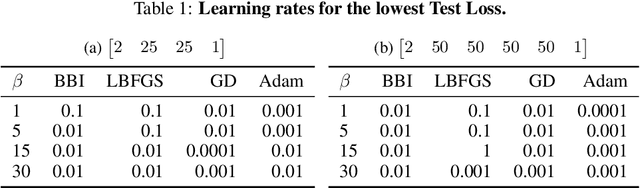
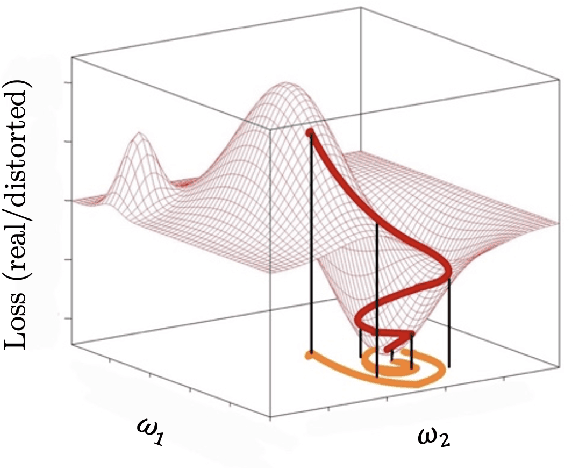
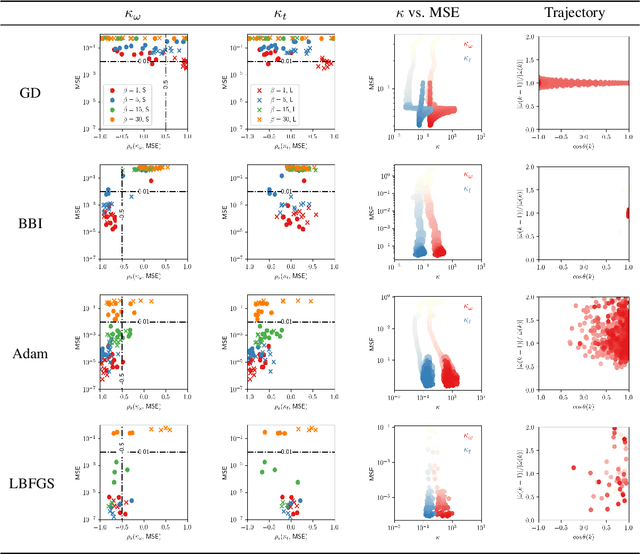
A novel comparison is presented of the effect of optimiser choice on the accuracy of physics-informed neural networks (PINNs). To give insight into why some optimisers are better, a new approach is proposed that tracks the training trajectory curvature and can be evaluated on the fly at a low computational cost. The linear advection equation is studied for several advective velocities, and we show that the optimiser choice substantially impacts PINNs model performance and accuracy. Furthermore, using the curvature measure, we found a negative correlation between the convergence error and the curvature in the optimiser local reference frame. It is concluded that, in this case, larger local curvature values result in better solutions. Consequently, optimisation of PINNs is made more difficult as minima are in highly curved regions.

Similarity and Generalization: From Noise to Corruption

Contrastive learning aims to extract distinctive features from data by finding an embedding representation where similar samples are close to each other, and different ones are far apart. We study generalization in contrastive learning, focusing on its simplest representative: Siamese Neural Networks (SNNs). We show that Double Descent also appears in SNNs and is exacerbated by noise. We point out that SNNs can be affected by two distinct sources of noise: Pair Label Noise (PLN) and Single Label Noise (SLN). The effect of SLN is asymmetric, but it preserves similarity relations, while PLN is symmetric but breaks transitivity. We show that the dataset topology crucially affects generalization. While sparse datasets show the same performances under SLN and PLN for an equal amount of noise, SLN outperforms PLN in the overparametrized region in dense datasets. Indeed, in this regime, PLN similarity violation becomes macroscopical, corrupting the dataset to the point where complete overfitting cannot be achieved. We call this phenomenon Density-Induced Break of Similarity (DIBS). We also probe the equivalence between online optimization and offline generalization for similarity tasks. We observe that an online/offline correspondence in similarity learning can be affected by both the network architecture and label noise.

dNNsolve: an efficient NN-based PDE solver

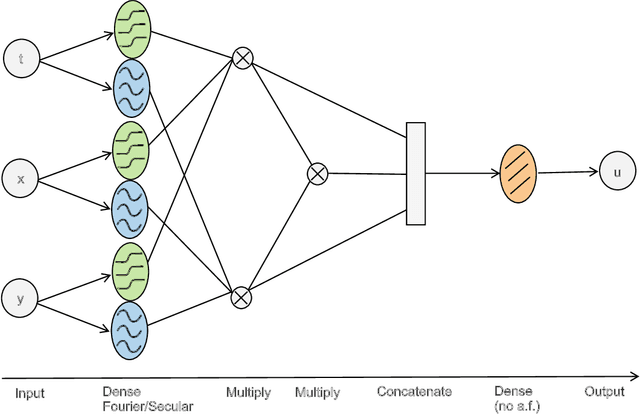
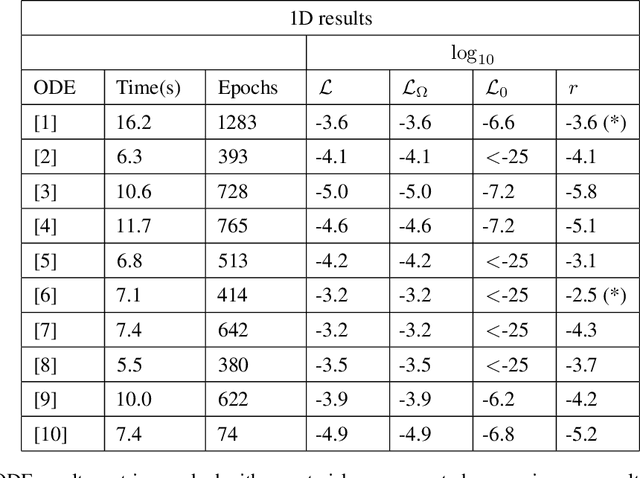
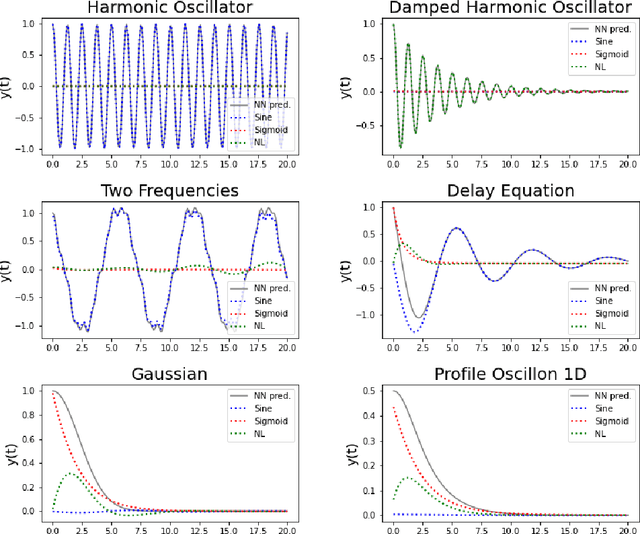
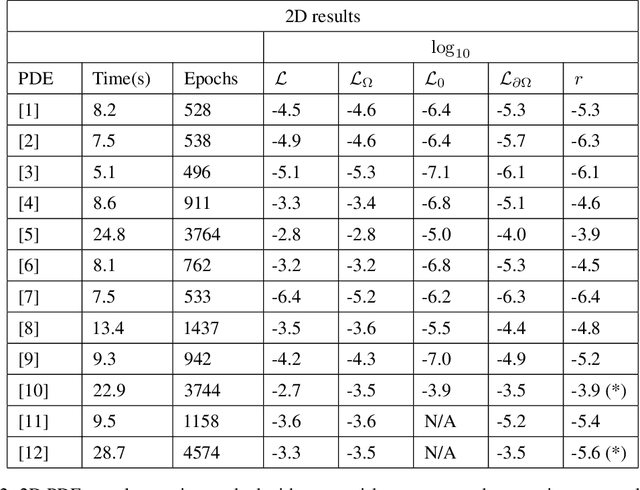
Neural Networks (NNs) can be used to solve Ordinary and Partial Differential Equations (ODEs and PDEs) by redefining the question as an optimization problem. The objective function to be optimized is the sum of the squares of the PDE to be solved and of the initial/boundary conditions. A feed forward NN is trained to minimise this loss function evaluated on a set of collocation points sampled from the domain where the problem is defined. A compact and smooth solution, that only depends on the weights of the trained NN, is then obtained. This approach is often referred to as PINN, from Physics Informed Neural Network~\cite{raissi2017physics_1, raissi2017physics_2}. Despite the success of the PINN approach in solving various classes of PDEs, an implementation of this idea that is capable of solving a large class of ODEs and PDEs with good accuracy and without the need to finely tune the hyperparameters of the network, is not available yet. In this paper, we introduce a new implementation of this concept - called dNNsolve - that makes use of dual Neural Networks to solve ODEs/PDEs. These include: i) sine and sigmoidal activation functions, that provide a more efficient basis to capture both secular and periodic patterns in the solutions; ii) a newly designed architecture, that makes it easy for the the NN to approximate the solution using the basis functions mentioned above. We show that dNNsolve is capable of solving a broad range of ODEs/PDEs in 1, 2 and 3 spacetime dimensions, without the need of hyperparameter fine-tuning.