dNNsolve: an efficient NN-based PDE solver
Paper and Code
Mar 15, 2021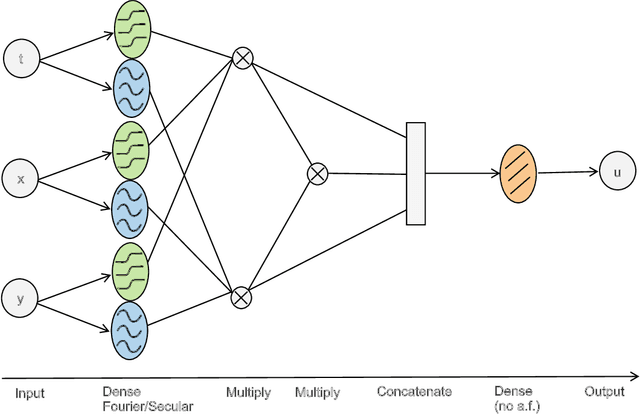
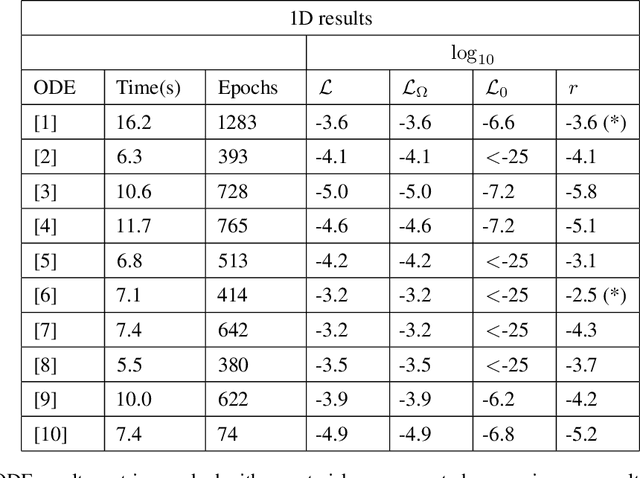
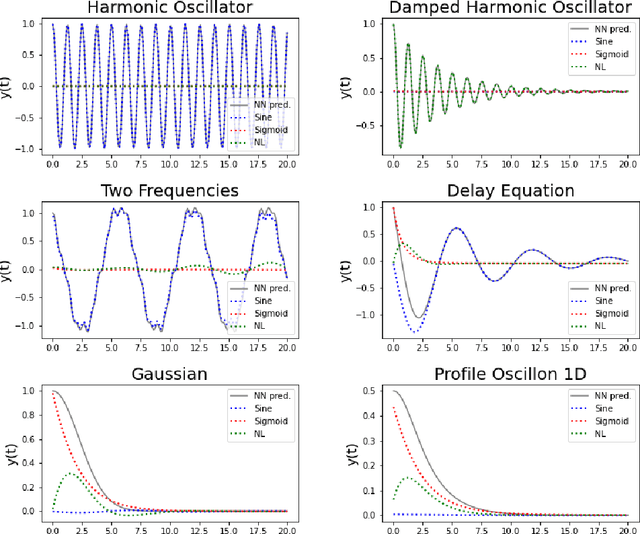
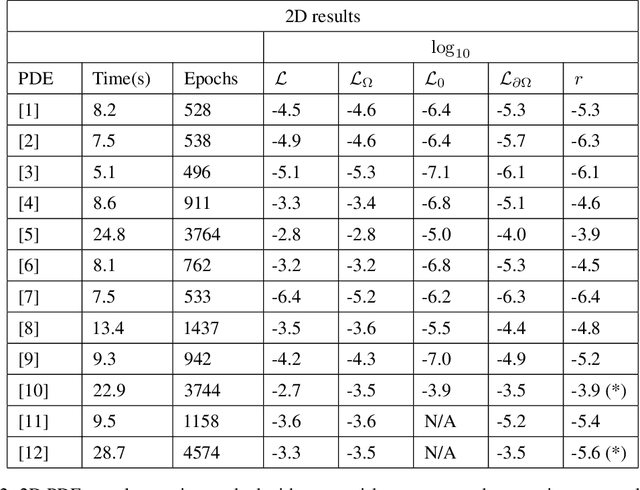
Neural Networks (NNs) can be used to solve Ordinary and Partial Differential Equations (ODEs and PDEs) by redefining the question as an optimization problem. The objective function to be optimized is the sum of the squares of the PDE to be solved and of the initial/boundary conditions. A feed forward NN is trained to minimise this loss function evaluated on a set of collocation points sampled from the domain where the problem is defined. A compact and smooth solution, that only depends on the weights of the trained NN, is then obtained. This approach is often referred to as PINN, from Physics Informed Neural Network~\cite{raissi2017physics_1, raissi2017physics_2}. Despite the success of the PINN approach in solving various classes of PDEs, an implementation of this idea that is capable of solving a large class of ODEs and PDEs with good accuracy and without the need to finely tune the hyperparameters of the network, is not available yet. In this paper, we introduce a new implementation of this concept - called dNNsolve - that makes use of dual Neural Networks to solve ODEs/PDEs. These include: i) sine and sigmoidal activation functions, that provide a more efficient basis to capture both secular and periodic patterns in the solutions; ii) a newly designed architecture, that makes it easy for the the NN to approximate the solution using the basis functions mentioned above. We show that dNNsolve is capable of solving a broad range of ODEs/PDEs in 1, 2 and 3 spacetime dimensions, without the need of hyperparameter fine-tuning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge