An exactly solvable model for emergence and scaling laws

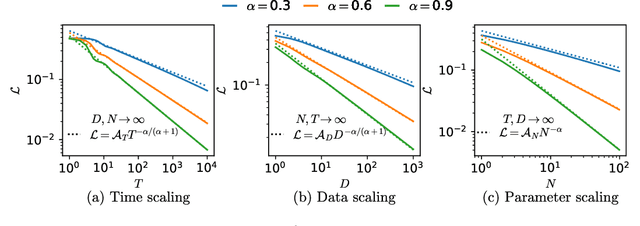
Deep learning models can exhibit what appears to be a sudden ability to solve a new problem as training time ($T$), training data ($D$), or model size ($N$) increases, a phenomenon known as emergence. In this paper, we present a framework where each new ability (a skill) is represented as a basis function. We solve a simple multi-linear model in this skill-basis, finding analytic expressions for the emergence of new skills, as well as for scaling laws of the loss with training time, data size, model size, and optimal compute ($C$). We compare our detailed calculations to direct simulations of a two-layer neural network trained on multitask sparse parity, where the tasks in the dataset are distributed according to a power-law. Our simple model captures, using a single fit parameter, the sigmoidal emergence of multiple new skills as training time, data size or model size increases in the neural network.

Probing optimisation in physics-informed neural networks

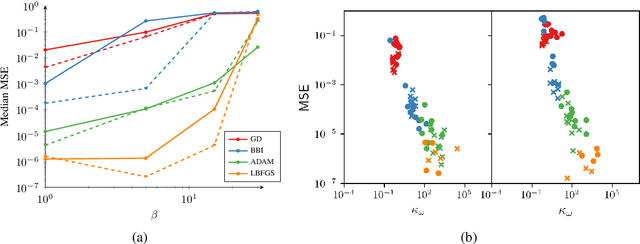
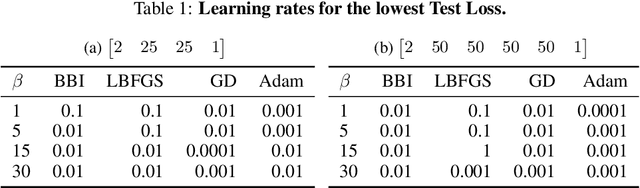
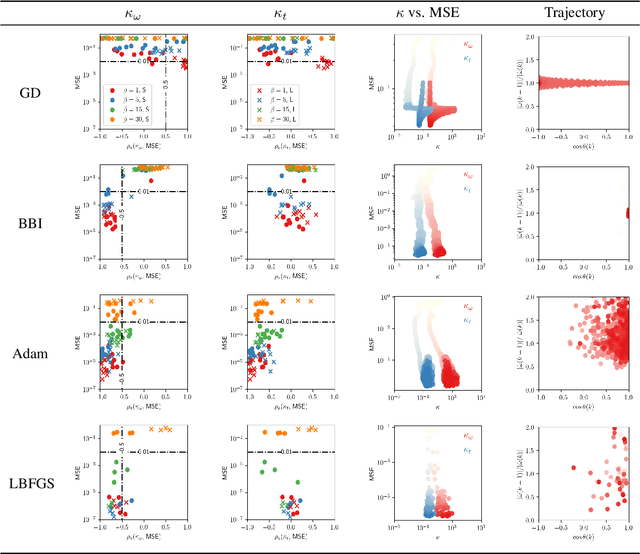
A novel comparison is presented of the effect of optimiser choice on the accuracy of physics-informed neural networks (PINNs). To give insight into why some optimisers are better, a new approach is proposed that tracks the training trajectory curvature and can be evaluated on the fly at a low computational cost. The linear advection equation is studied for several advective velocities, and we show that the optimiser choice substantially impacts PINNs model performance and accuracy. Furthermore, using the curvature measure, we found a negative correlation between the convergence error and the curvature in the optimiser local reference frame. It is concluded that, in this case, larger local curvature values result in better solutions. Consequently, optimisation of PINNs is made more difficult as minima are in highly curved regions.

Similarity and Generalization: From Noise to Corruption

Contrastive learning aims to extract distinctive features from data by finding an embedding representation where similar samples are close to each other, and different ones are far apart. We study generalization in contrastive learning, focusing on its simplest representative: Siamese Neural Networks (SNNs). We show that Double Descent also appears in SNNs and is exacerbated by noise. We point out that SNNs can be affected by two distinct sources of noise: Pair Label Noise (PLN) and Single Label Noise (SLN). The effect of SLN is asymmetric, but it preserves similarity relations, while PLN is symmetric but breaks transitivity. We show that the dataset topology crucially affects generalization. While sparse datasets show the same performances under SLN and PLN for an equal amount of noise, SLN outperforms PLN in the overparametrized region in dense datasets. Indeed, in this regime, PLN similarity violation becomes macroscopical, corrupting the dataset to the point where complete overfitting cannot be achieved. We call this phenomenon Density-Induced Break of Similarity (DIBS). We also probe the equivalence between online optimization and offline generalization for similarity tasks. We observe that an online/offline correspondence in similarity learning can be affected by both the network architecture and label noise.