An exactly solvable model for emergence and scaling laws
Paper and Code
Apr 26, 2024

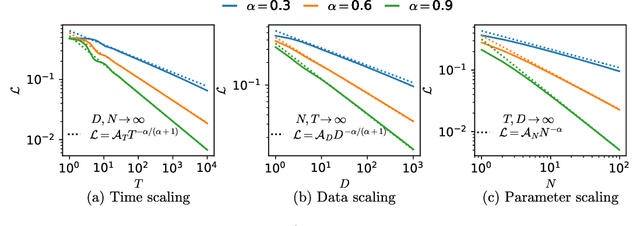

Deep learning models can exhibit what appears to be a sudden ability to solve a new problem as training time ($T$), training data ($D$), or model size ($N$) increases, a phenomenon known as emergence. In this paper, we present a framework where each new ability (a skill) is represented as a basis function. We solve a simple multi-linear model in this skill-basis, finding analytic expressions for the emergence of new skills, as well as for scaling laws of the loss with training time, data size, model size, and optimal compute ($C$). We compare our detailed calculations to direct simulations of a two-layer neural network trained on multitask sparse parity, where the tasks in the dataset are distributed according to a power-law. Our simple model captures, using a single fit parameter, the sigmoidal emergence of multiple new skills as training time, data size or model size increases in the neural network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge