Position: Many generalization measures for deep learning are fragile

A wide variety of generalization measures have been applied to deep neural networks (DNNs). Although obtaining tight bounds remains challenging, such measures are often assumed to reproduce qualitative generalization trends. In this position paper, we argue that many post-mortem generalization measures -- those computed on trained networks -- are \textbf{fragile}: small training modifications that barely affect the underlying DNN can substantially change a measure's value, trend, or scaling behavior. For example, minor hyperparameter changes, such as learning rate adjustments or switching between SGD variants can reverse the slope of a learning curve in widely used generalization measures like the path norm. We also identify subtler forms of fragility. For instance, the PAC-Bayes origin measure is regarded as one of the most reliable, and is indeed less sensitive to hyperparameter tweaks than many other measures. However, it completely fails to capture differences in data complexity across learning curves. This data fragility contrasts with the function-based marginal-likelihood PAC-Bayes bound, which does capture differences in data-complexity, including scaling behavior, in learning curves, but which is not a post-mortem measure. Beyond demonstrating that many bounds -- such as path, spectral and Frobenius norms, flatness proxies, and deterministic PAC-Bayes surrogates -- are fragile, this position paper also argues that developers of new measures should explicitly audit them for fragility.

Characterising the Inductive Biases of Neural Networks on Boolean Data

Deep neural networks are renowned for their ability to generalise well across diverse tasks, even when heavily overparameterized. Existing works offer only partial explanations (for example, the NTK-based task-model alignment explanation neglects feature learning). Here, we provide an end-to-end, analytically tractable case study that links a network's inductive prior, its training dynamics including feature learning, and its eventual generalisation. Specifically, we exploit the one-to-one correspondence between depth-2 discrete fully connected networks and disjunctive normal form (DNF) formulas by training on Boolean functions. Under a Monte Carlo learning algorithm, our model exhibits predictable training dynamics and the emergence of interpretable features. This framework allows us to trace, in detail, how inductive bias and feature formation drive generalisation.

Visualising Feature Learning in Deep Neural Networks by Diagonalizing the Forward Feature Map

Deep neural networks (DNNs) exhibit a remarkable ability to automatically learn data representations, finding appropriate features without human input. Here we present a method for analysing feature learning by decomposing DNNs into 1) a forward feature-map $\Phi$ that maps the input dataspace to the post-activations of the penultimate layer, and 2) a final linear layer that classifies the data. We diagonalize $\Phi$ with respect to the gradient descent operator and track feature learning by measuring how the eigenfunctions and eigenvalues of $\Phi$ change during training. Across many popular architectures and classification datasets, we find that DNNs converge, after just a few epochs, to a minimal feature (MF) regime dominated by a number of eigenfunctions equal to the number of classes. This behaviour resembles the neural collapse phenomenon studied at longer training times. For other DNN-data combinations, such as a fully connected network on CIFAR10, we find an extended feature (EF) regime where significantly more features are used. Optimal generalisation performance upon hyperparameter tuning typically coincides with the MF regime, but we also find examples of poor performance within the MF regime. Finally, we recast the phenomenon of neural collapse into a kernel picture which can be extended to broader tasks such as regression.

An exactly solvable model for emergence and scaling laws

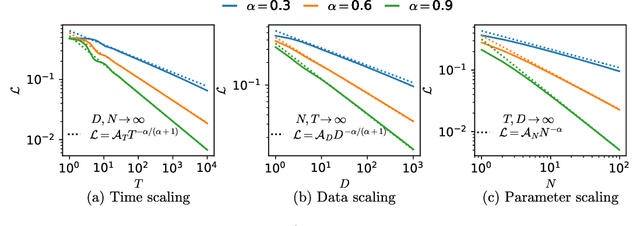
Deep learning models can exhibit what appears to be a sudden ability to solve a new problem as training time ($T$), training data ($D$), or model size ($N$) increases, a phenomenon known as emergence. In this paper, we present a framework where each new ability (a skill) is represented as a basis function. We solve a simple multi-linear model in this skill-basis, finding analytic expressions for the emergence of new skills, as well as for scaling laws of the loss with training time, data size, model size, and optimal compute ($C$). We compare our detailed calculations to direct simulations of a two-layer neural network trained on multitask sparse parity, where the tasks in the dataset are distributed according to a power-law. Our simple model captures, using a single fit parameter, the sigmoidal emergence of multiple new skills as training time, data size or model size increases in the neural network.

Why Flatness Correlates With Generalization For Deep Neural Networks

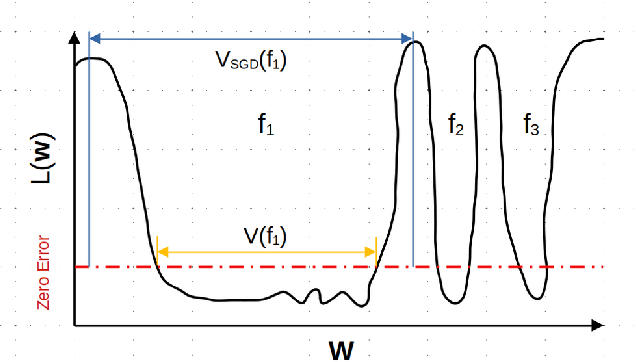
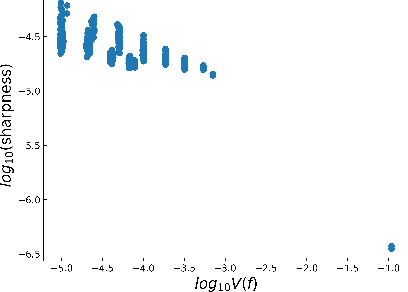
The intuition that local flatness of the loss landscape is correlated with better generalization for deep neural networks (DNNs) has been explored for decades, spawning many different local flatness measures. Here we argue that these measures correlate with generalization because they are local approximations to a global property, the volume of the set of parameters mapping to a specific function. This global volume is equivalent to the Bayesian prior upon initialization. For functions that give zero error on a test set, it is directly proportional to the Bayesian posterior, making volume a more robust and theoretically better grounded predictor of generalization than flatness. Whilst flatness measures fail under parameter re-scaling, volume remains invariant and therefore continues to correlate well with generalization. Moreover, some variants of SGD can break the flatness-generalization correlation, while the volume-generalization correlation remains intact.