Preference Alignment with Flow Matching

We present Preference Flow Matching (PFM), a new framework for preference-based reinforcement learning (PbRL) that streamlines the integration of preferences into an arbitrary class of pre-trained models. Existing PbRL methods require fine-tuning pre-trained models, which presents challenges such as scalability, inefficiency, and the need for model modifications, especially with black-box APIs like GPT-4. In contrast, PFM utilizes flow matching techniques to directly learn from preference data, thereby reducing the dependency on extensive fine-tuning of pre-trained models. By leveraging flow-based models, PFM transforms less preferred data into preferred outcomes, and effectively aligns model outputs with human preferences without relying on explicit or implicit reward function estimation, thus avoiding common issues like overfitting in reward models. We provide theoretical insights that support our method's alignment with standard PbRL objectives. Experimental results indicate the practical effectiveness of our method, offering a new direction in aligning a pre-trained model to preference.

Mold into a Graph: Efficient Bayesian Optimization over Mixed-Spaces

Real-world optimization problems are generally not just black-box problems, but also involve mixed types of inputs in which discrete and continuous variables coexist. Such mixed-space optimization possesses the primary challenge of modeling complex interactions between the inputs. In this work, we propose a novel yet simple approach that entails exploiting the graph data structure to model the underlying relationship between variables, i.e., variables as nodes and interactions defined by edges. Then, a variational graph autoencoder is used to naturally take the interactions into account. We first provide empirical evidence of the existence of such graph structures and then suggest a joint framework of graph structure learning and latent space optimization to adaptively search for optimal graph connectivity. Experimental results demonstrate that our method shows remarkable performance, exceeding the existing approaches with significant computational efficiency for a number of synthetic and real-world tasks.

Meta-learning Amidst Heterogeneity and Ambiguity

Meta-learning aims to learn a model that can handle multiple tasks generated from an unknown but shared distribution. However, typical meta-learning algorithms have assumed the tasks to be similar such that a single meta-learner is sufficient to aggregate the variations in all aspects. In addition, there has been less consideration on uncertainty when limited information is given as context. In this paper, we devise a novel meta-learning framework, called Meta-learning Amidst Heterogeneity and Ambiguity (MAHA), that outperforms previous works in terms of prediction based on its ability on task identification. By extensively conducting several experiments in regression and classification, we demonstrate the validity of our model, which turns out to be robust to both task heterogeneity and ambiguity.

Adaptive Local Bayesian Optimization Over Multiple Discrete Variables

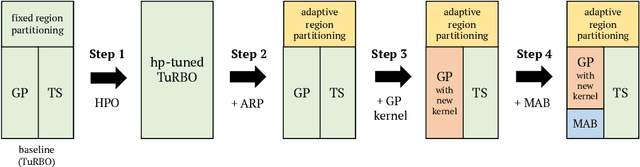
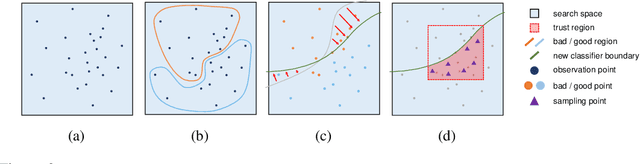
In the machine learning algorithms, the choice of the hyperparameter is often an art more than a science, requiring labor-intensive search with expert experience. Therefore, automation on hyperparameter optimization to exclude human intervention is a great appeal, especially for the black-box functions. Recently, there have been increasing demands of solving such concealed tasks for better generalization, though the task-dependent issue is not easy to solve. The Black-Box Optimization challenge (NeurIPS 2020) required competitors to build a robust black-box optimizer across different domains of standard machine learning problems. This paper describes the approach of team KAIST OSI in a step-wise manner, which outperforms the baseline algorithms by up to +20.39%. We first strengthen the local Bayesian search under the concept of region reliability. Then, we design a combinatorial kernel for a Gaussian process kernel. In a similar vein, we combine the methodology of Bayesian and multi-armed bandit,(MAB) approach to select the values with the consideration of the variable types; the real and integer variables are with Bayesian, while the boolean and categorical variables are with MAB. Empirical evaluations demonstrate that our method outperforms the existing methods across different tasks.

Accurate and Fast Federated Learning via Combinatorial Multi-Armed Bandits

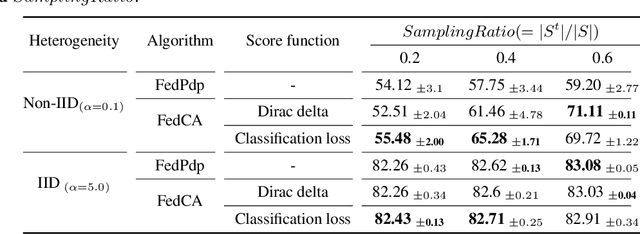
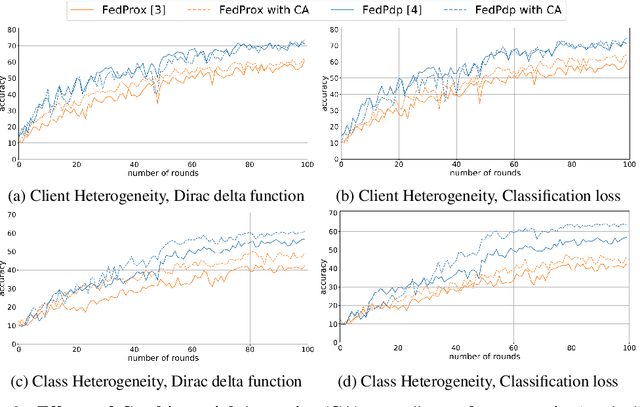
Federated learning has emerged as an innovative paradigm of collaborative machine learning. Unlike conventional machine learning, a global model is collaboratively learned while data remains distributed over a tremendous number of client devices, thus not compromising user privacy. However, several challenges still remain despite its glowing popularity; above all, the global aggregation in federated learning involves the challenge of biased model averaging and lack of prior knowledge in client sampling, which, in turn, leads to high generalization error and slow convergence rate, respectively. In this work, we propose a novel algorithm called FedCM that addresses the two challenges by utilizing prior knowledge with multi-armed bandit based client sampling and filtering biased models with combinatorial model averaging. Based on extensive evaluations using various algorithms and representative heterogeneous datasets, we showed that FedCM significantly outperformed the state-of-the-art algorithms by up to 37.25% and 4.17 times, respectively, in terms of generalization accuracy and convergence rate.

Convergence Rates of Gradient Descent and MM Algorithms for Generalized Bradley-Terry Models

We show tight convergence rate bounds for gradient descent and MM algorithms for maximum likelihood estimation and maximum aposteriori probability estimation of a popular Bayesian inference method for generalized Bradley-Terry models. This class of models includes the Bradley-Terry model of paired comparisons, the Rao-Kupper model of paired comparisons with ties, the Luce choice model, and the Plackett-Luce ranking model. Our results show that MM algorithms have same convergence rates as gradient descent algorithms up to constant factors. For the maximum likelihood estimation, the convergence is linear with the rate crucially determined by the algebraic connectivity of the matrix of item pair co-occurrences in observed comparison data. For the Bayesian inference, the convergence rate is also linear, with the rate determined by a parameter of the prior distribution in a way that can make convergence arbitrarily slow for small values of this parameter. We propose a simple, first-order acceleration method that resolves the slow convergence issue.