Mold into a Graph: Efficient Bayesian Optimization over Mixed-Spaces

Real-world optimization problems are generally not just black-box problems, but also involve mixed types of inputs in which discrete and continuous variables coexist. Such mixed-space optimization possesses the primary challenge of modeling complex interactions between the inputs. In this work, we propose a novel yet simple approach that entails exploiting the graph data structure to model the underlying relationship between variables, i.e., variables as nodes and interactions defined by edges. Then, a variational graph autoencoder is used to naturally take the interactions into account. We first provide empirical evidence of the existence of such graph structures and then suggest a joint framework of graph structure learning and latent space optimization to adaptively search for optimal graph connectivity. Experimental results demonstrate that our method shows remarkable performance, exceeding the existing approaches with significant computational efficiency for a number of synthetic and real-world tasks.

Adaptive Local Bayesian Optimization Over Multiple Discrete Variables

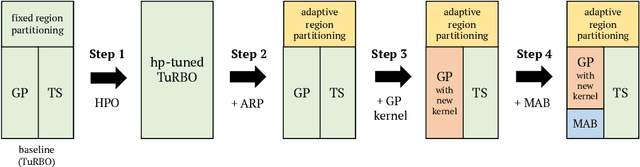
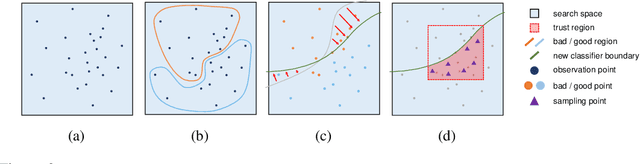
In the machine learning algorithms, the choice of the hyperparameter is often an art more than a science, requiring labor-intensive search with expert experience. Therefore, automation on hyperparameter optimization to exclude human intervention is a great appeal, especially for the black-box functions. Recently, there have been increasing demands of solving such concealed tasks for better generalization, though the task-dependent issue is not easy to solve. The Black-Box Optimization challenge (NeurIPS 2020) required competitors to build a robust black-box optimizer across different domains of standard machine learning problems. This paper describes the approach of team KAIST OSI in a step-wise manner, which outperforms the baseline algorithms by up to +20.39%. We first strengthen the local Bayesian search under the concept of region reliability. Then, we design a combinatorial kernel for a Gaussian process kernel. In a similar vein, we combine the methodology of Bayesian and multi-armed bandit,(MAB) approach to select the values with the consideration of the variable types; the real and integer variables are with Bayesian, while the boolean and categorical variables are with MAB. Empirical evaluations demonstrate that our method outperforms the existing methods across different tasks.