COLOGNE: Coordinated Local Graph Neighborhood Sampling
Paper and Code
Feb 09, 2021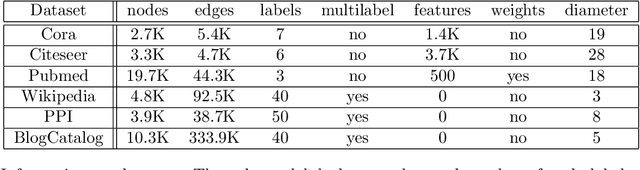

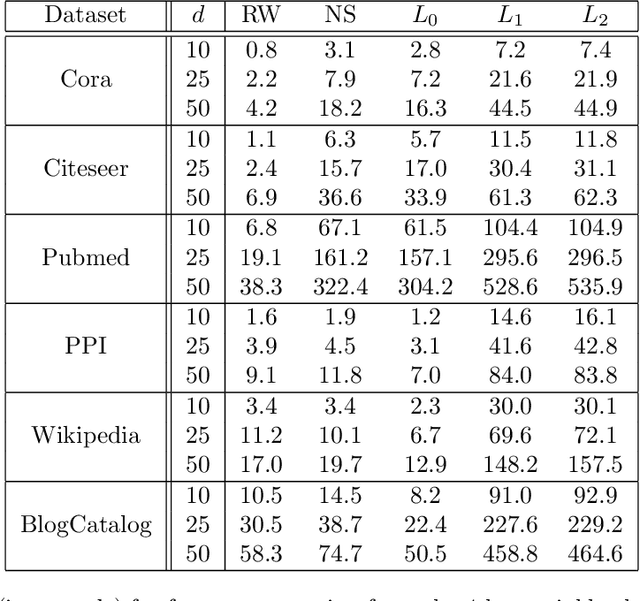
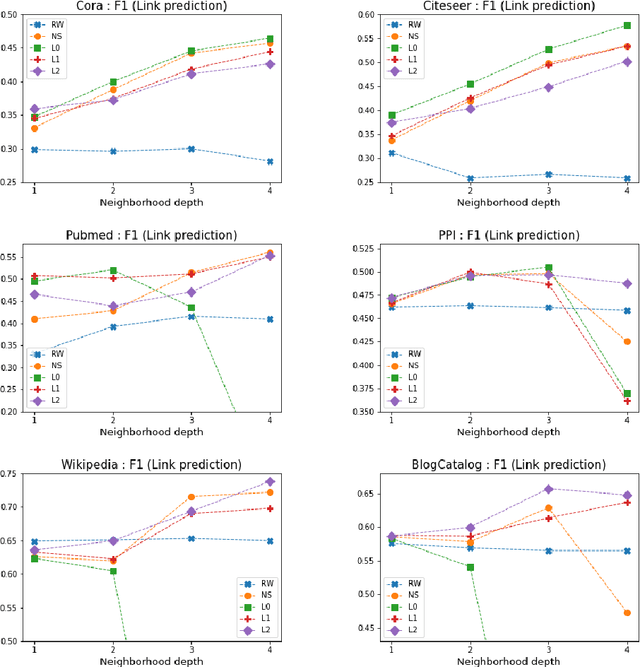
Representation learning for graphs enables the application of standard machine learning algorithms and data analysis tools to graph data. Replacing discrete unordered objects such as graph nodes by real-valued vectors is at the heart of many approaches to learning from graph data. Such vector representations, or embeddings, capture the discrete relationships in the original data by representing nodes as vectors in a high-dimensional space. In most applications graphs model the relationship between real-life objects and often nodes contain valuable meta-information about the original objects. While being a powerful machine learning tool, embeddings are not able to preserve such node attributes. We address this shortcoming and consider the problem of learning discrete node embeddings such that the coordinates of the node vector representations are graph nodes. This opens the door to designing interpretable machine learning algorithms for graphs as all attributes originally present in the nodes are preserved. We present a framework for coordinated local graph neighborhood sampling (COLOGNE) such that each node is represented by a fixed number of graph nodes, together with their attributes. Individual samples are coordinated and they preserve the similarity between node neighborhoods. We consider different notions of similarity for which we design scalable algorithms. We show theoretical results for all proposed algorithms. Experiments on benchmark graphs evaluate the quality of the designed embeddings and demonstrate how the proposed embeddings can be used in training interpretable machine learning algorithms for graph data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge