Query-Efficient Correlation Clustering
Paper and Code
Feb 26, 2020
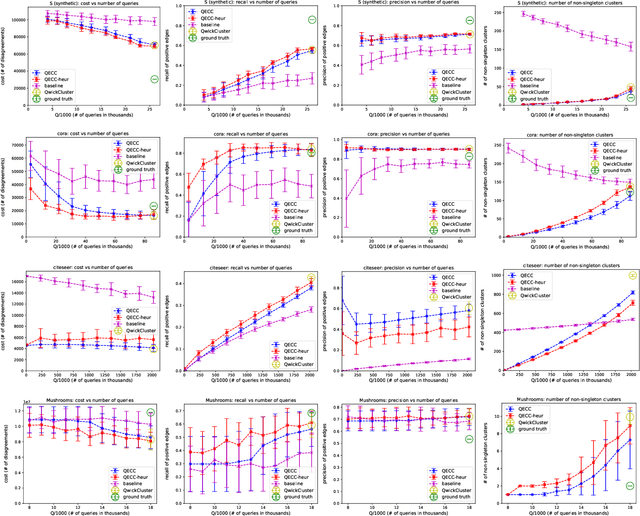
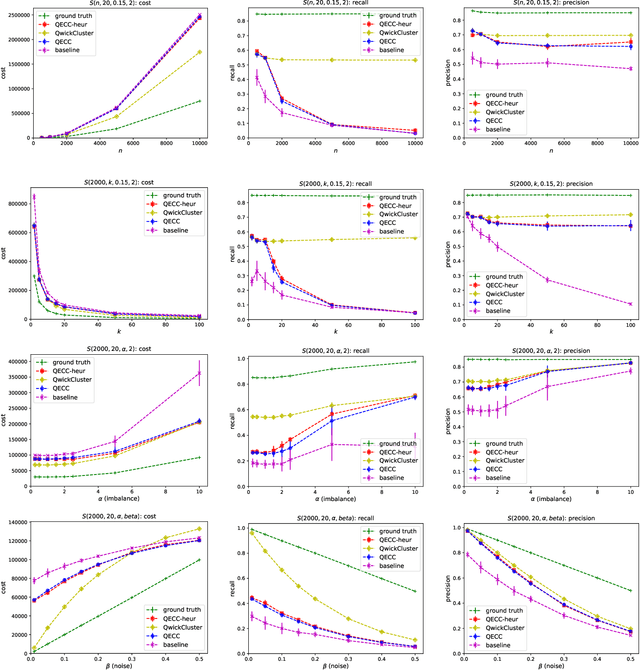
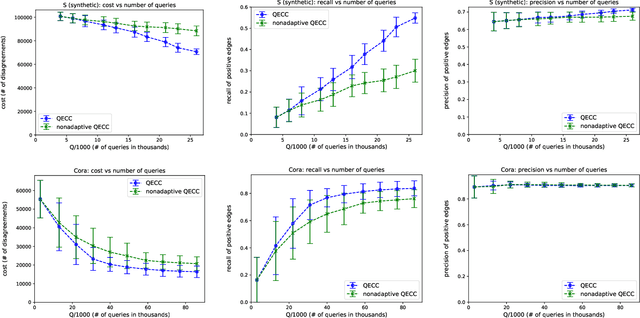
Correlation clustering is arguably the most natural formulation of clustering. Given n objects and a pairwise similarity measure, the goal is to cluster the objects so that, to the best possible extent, similar objects are put in the same cluster and dissimilar objects are put in different clusters. A main drawback of correlation clustering is that it requires as input the $\Theta(n^2)$ pairwise similarities. This is often infeasible to compute or even just to store. In this paper we study \emph{query-efficient} algorithms for correlation clustering. Specifically, we devise a correlation clustering algorithm that, given a budget of $Q$ queries, attains a solution whose expected number of disagreements is at most $3\cdot OPT + O(\frac{n^3}{Q})$, where $OPT$ is the optimal cost for the instance. Its running time is $O(Q)$, and can be easily made non-adaptive (meaning it can specify all its queries at the outset and make them in parallel) with the same guarantees. Up to constant factors, our algorithm yields a provably optimal trade-off between the number of queries $Q$ and the worst-case error attained, even for adaptive algorithms. Finally, we perform an experimental study of our proposed method on both synthetic and real data, showing the scalability and the accuracy of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge