Sharper Bounds for Chebyshev Moment Matching with Applications to Differential Privacy and Beyond

We study the problem of approximately recovering a probability distribution given noisy measurements of its Chebyshev polynomial moments. We sharpen prior work, proving that accurate recovery in the Wasserstein distance is possible with more noise than previously known. As a main application, our result yields a simple "linear query" algorithm for constructing a differentially private synthetic data distribution with Wasserstein-1 error $\tilde{O}(1/n)$ based on a dataset of $n$ points in $[-1,1]$. This bound is optimal up to log factors and matches a recent breakthrough of Boedihardjo, Strohmer, and Vershynin [Probab. Theory. Rel., 2024], which uses a more complex "superregular random walk" method to beat an $O(1/\sqrt{n})$ accuracy barrier inherent to earlier approaches. We illustrate a second application of our new moment-based recovery bound in numerical linear algebra: by improving an approach of Braverman, Krishnan, and Musco [STOC 2022], our result yields a faster algorithm for estimating the spectral density of a symmetric matrix up to small error in the Wasserstein distance.

Faster Spectral Density Estimation and Sparsification in the Nuclear Norm

We consider the problem of estimating the spectral density of the normalized adjacency matrix of an $n$-node undirected graph. We provide a randomized algorithm that, with $O(n\epsilon^{-2})$ queries to a degree and neighbor oracle and in $O(n\epsilon^{-3})$ time, estimates the spectrum up to $\epsilon$ accuracy in the Wasserstein-1 metric. This improves on previous state-of-the-art methods, including an $O(n\epsilon^{-7})$ time algorithm from [Braverman et al., STOC 2022] and, for sufficiently small $\epsilon$, a $2^{O(\epsilon^{-1})}$ time method from [Cohen-Steiner et al., KDD 2018]. To achieve this result, we introduce a new notion of graph sparsification, which we call nuclear sparsification. We provide an $O(n\epsilon^{-2})$-query and $O(n\epsilon^{-2})$-time algorithm for computing $O(n\epsilon^{-2})$-sparse nuclear sparsifiers. We show that this bound is optimal in both its sparsity and query complexity, and we separate our results from the related notion of additive spectral sparsification. Of independent interest, we show that our sparsification method also yields the first deterministic algorithm for spectral density estimation that scales linearly with $n$ (sublinear in the representation size of the graph).

Moments, Random Walks, and Limits for Spectrum Approximation

We study lower bounds for the problem of approximating a one dimensional distribution given (noisy) measurements of its moments. We show that there are distributions on $[-1,1]$ that cannot be approximated to accuracy $\epsilon$ in Wasserstein-1 distance even if we know \emph{all} of their moments to multiplicative accuracy $(1\pm2^{-\Omega(1/\epsilon)})$; this result matches an upper bound of Kong and Valiant [Annals of Statistics, 2017]. To obtain our result, we provide a hard instance involving distributions induced by the eigenvalue spectra of carefully constructed graph adjacency matrices. Efficiently approximating such spectra in Wasserstein-1 distance is a well-studied algorithmic problem, and a recent result of Cohen-Steiner et al. [KDD 2018] gives a method based on accurately approximating spectral moments using $2^{O(1/\epsilon)}$ random walks initiated at uniformly random nodes in the graph. As a strengthening of our main result, we show that improving the dependence on $1/\epsilon$ in this result would require a new algorithmic approach. Specifically, no algorithm can compute an $\epsilon$-accurate approximation to the spectrum of a normalized graph adjacency matrix with constant probability, even when given the transcript of $2^{\Omega(1/\epsilon)}$ random walks of length $2^{\Omega(1/\epsilon)}$ started at random nodes.

Regularized spectral methods for clustering signed networks

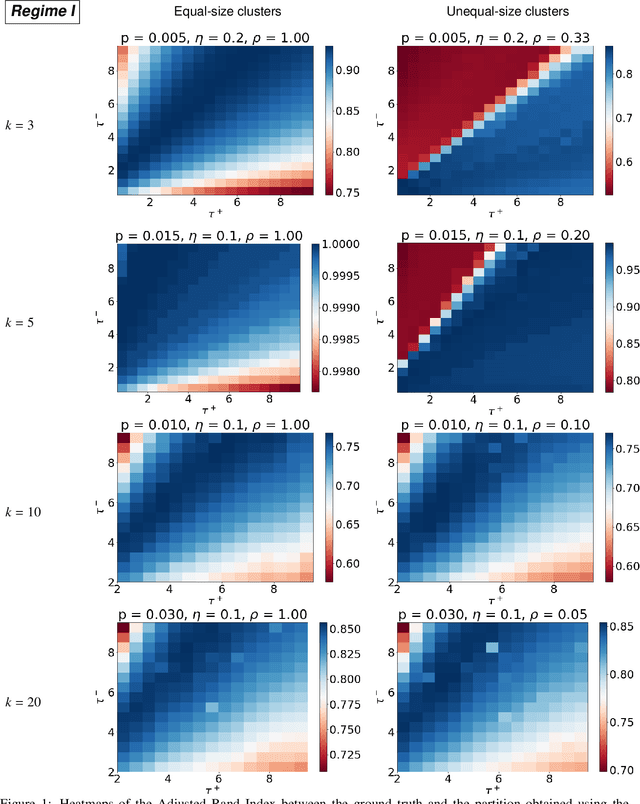
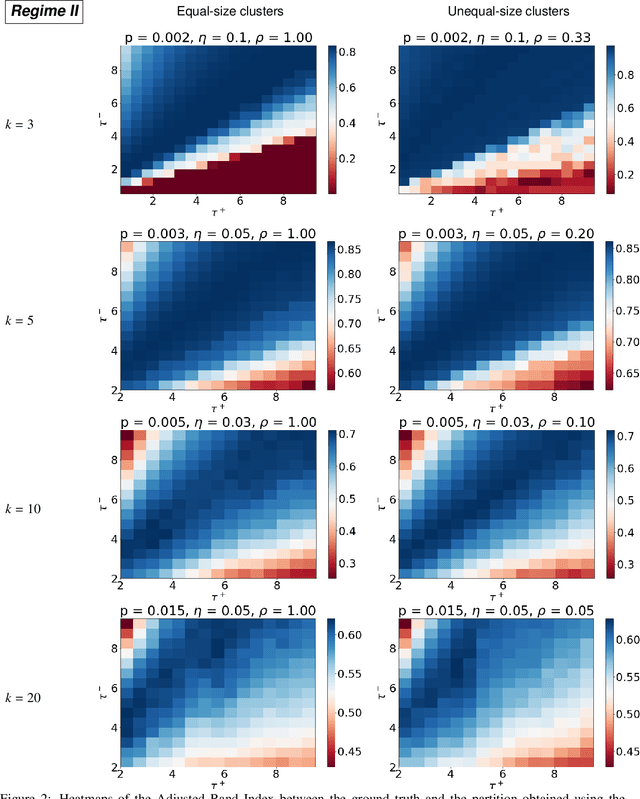
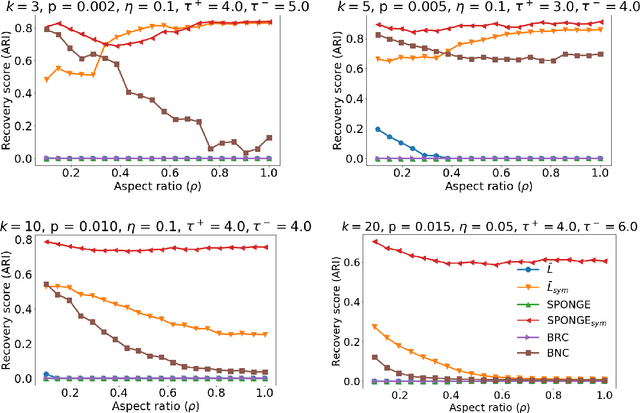
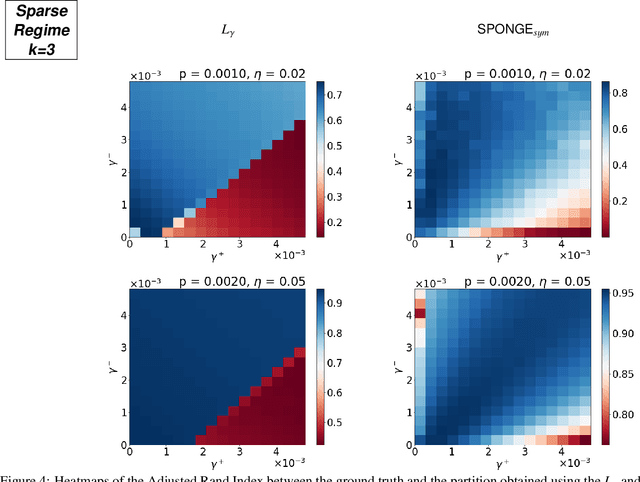
We study the problem of $k$-way clustering in signed graphs. Considerable attention in recent years has been devoted to analyzing and modeling signed graphs, where the affinity measure between nodes takes either positive or negative values. Recently, Cucuringu et al. [CDGT 2019] proposed a spectral method, namely SPONGE (Signed Positive over Negative Generalized Eigenproblem), which casts the clustering task as a generalized eigenvalue problem optimizing a suitably defined objective function. This approach is motivated by social balance theory, where the clustering task aims to decompose a given network into disjoint groups, such that individuals within the same group are connected by as many positive edges as possible, while individuals from different groups are mainly connected by negative edges. Through extensive numerical simulations, SPONGE was shown to achieve state-of-the-art empirical performance. On the theoretical front, [CDGT 2019] analyzed SPONGE and the popular Signed Laplacian method under the setting of a Signed Stochastic Block Model (SSBM), for $k=2$ equal-sized clusters, in the regime where the graph is moderately dense. In this work, we build on the results in [CDGT 2019] on two fronts for the normalized versions of SPONGE and the Signed Laplacian. Firstly, for both algorithms, we extend the theoretical analysis in [CDGT 2019] to the general setting of $k \geq 2$ unequal-sized clusters in the moderately dense regime. Secondly, we introduce regularized versions of both methods to handle sparse graphs -- a regime where standard spectral methods underperform -- and provide theoretical guarantees under the same SSBM model. To the best of our knowledge, regularized spectral methods have so far not been considered in the setting of clustering signed graphs. We complement our theoretical results with an extensive set of numerical experiments on synthetic data.

On Euclidean $k$-Means Clustering with $α$-Center Proximity

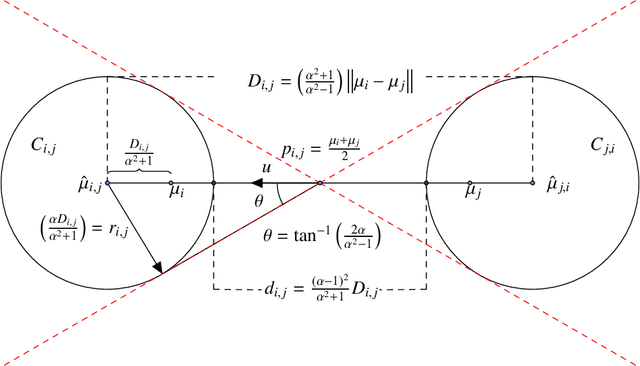
The $k$-means is a popular clustering objective that is NP-hard in the worst-case but often solved efficiently by simple heuristics in practice. The implicit assumption behind using the $k$-means (or many other objectives) is that an optimal solution would recover the underlying ground truth clustering. In most real-world datasets, the underlying ground-truth clustering is unambiguous and stable under small perturbations of data. As a consequence, the ground-truth clustering satisfies center proximity, that is, every point is closer to the center of its own cluster than the center of any other cluster, by some multiplicative factor $\alpha > 1$. We study the problem of minimizing the Euclidean $k$-means objective only over clusterings that satisfy $\alpha$-center proximity. We give a simple algorithm to find an exact optimal clustering for the above objective with running time exponential in $k$ and $1/(\alpha - 1)$ but linear in the number of points and the dimension. We define an analogous $\alpha$-center proximity condition for outliers, and give similar algorithmic guarantees for $k$-means with outliers and $\alpha$-center proximity. On the hardness side we show that for any $\alpha' > 1$, there exists an $\alpha \leq \alpha'$, $(\alpha >1)$, and an $\varepsilon_0 > 0$ such that minimizing the $k$-means objective over clusterings that satisfy $\alpha$-center proximity is NP-hard to approximate within a multiplicative $(1+\varepsilon_0)$ factor.