On Euclidean $k$-Means Clustering with $α$-Center Proximity
Paper and Code
Sep 06, 2018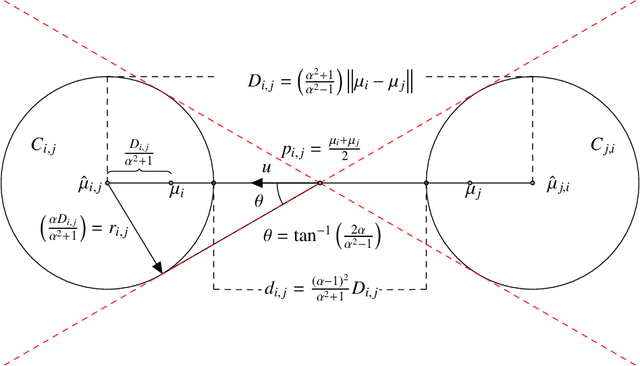
The $k$-means is a popular clustering objective that is NP-hard in the worst-case but often solved efficiently by simple heuristics in practice. The implicit assumption behind using the $k$-means (or many other objectives) is that an optimal solution would recover the underlying ground truth clustering. In most real-world datasets, the underlying ground-truth clustering is unambiguous and stable under small perturbations of data. As a consequence, the ground-truth clustering satisfies center proximity, that is, every point is closer to the center of its own cluster than the center of any other cluster, by some multiplicative factor $\alpha > 1$. We study the problem of minimizing the Euclidean $k$-means objective only over clusterings that satisfy $\alpha$-center proximity. We give a simple algorithm to find an exact optimal clustering for the above objective with running time exponential in $k$ and $1/(\alpha - 1)$ but linear in the number of points and the dimension. We define an analogous $\alpha$-center proximity condition for outliers, and give similar algorithmic guarantees for $k$-means with outliers and $\alpha$-center proximity. On the hardness side we show that for any $\alpha' > 1$, there exists an $\alpha \leq \alpha'$, $(\alpha >1)$, and an $\varepsilon_0 > 0$ such that minimizing the $k$-means objective over clusterings that satisfy $\alpha$-center proximity is NP-hard to approximate within a multiplicative $(1+\varepsilon_0)$ factor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge