GPT-4o System Card

GPT-4o is an autoregressive omni model that accepts as input any combination of text, audio, image, and video, and generates any combination of text, audio, and image outputs. It's trained end-to-end across text, vision, and audio, meaning all inputs and outputs are processed by the same neural network. GPT-4o can respond to audio inputs in as little as 232 milliseconds, with an average of 320 milliseconds, which is similar to human response time in conversation. It matches GPT-4 Turbo performance on text in English and code, with significant improvement on text in non-English languages, while also being much faster and 50\% cheaper in the API. GPT-4o is especially better at vision and audio understanding compared to existing models. In line with our commitment to building AI safely and consistent with our voluntary commitments to the White House, we are sharing the GPT-4o System Card, which includes our Preparedness Framework evaluations. In this System Card, we provide a detailed look at GPT-4o's capabilities, limitations, and safety evaluations across multiple categories, focusing on speech-to-speech while also evaluating text and image capabilities, and measures we've implemented to ensure the model is safe and aligned. We also include third-party assessments on dangerous capabilities, as well as discussion of potential societal impacts of GPT-4o's text and vision capabilities.

Faster Spectral Density Estimation and Sparsification in the Nuclear Norm

We consider the problem of estimating the spectral density of the normalized adjacency matrix of an $n$-node undirected graph. We provide a randomized algorithm that, with $O(n\epsilon^{-2})$ queries to a degree and neighbor oracle and in $O(n\epsilon^{-3})$ time, estimates the spectrum up to $\epsilon$ accuracy in the Wasserstein-1 metric. This improves on previous state-of-the-art methods, including an $O(n\epsilon^{-7})$ time algorithm from [Braverman et al., STOC 2022] and, for sufficiently small $\epsilon$, a $2^{O(\epsilon^{-1})}$ time method from [Cohen-Steiner et al., KDD 2018]. To achieve this result, we introduce a new notion of graph sparsification, which we call nuclear sparsification. We provide an $O(n\epsilon^{-2})$-query and $O(n\epsilon^{-2})$-time algorithm for computing $O(n\epsilon^{-2})$-sparse nuclear sparsifiers. We show that this bound is optimal in both its sparsity and query complexity, and we separate our results from the related notion of additive spectral sparsification. Of independent interest, we show that our sparsification method also yields the first deterministic algorithm for spectral density estimation that scales linearly with $n$ (sublinear in the representation size of the graph).

Truncated Variance Reduced Value Iteration

We provide faster randomized algorithms for computing an $\epsilon$-optimal policy in a discounted Markov decision process with $A_{\text{tot}}$-state-action pairs, bounded rewards, and discount factor $\gamma$. We provide an $\tilde{O}(A_{\text{tot}}[(1 - \gamma)^{-3}\epsilon^{-2} + (1 - \gamma)^{-2}])$-time algorithm in the sampling setting, where the probability transition matrix is unknown but accessible through a generative model which can be queried in $\tilde{O}(1)$-time, and an $\tilde{O}(s + (1-\gamma)^{-2})$-time algorithm in the offline setting where the probability transition matrix is known and $s$-sparse. These results improve upon the prior state-of-the-art which either ran in $\tilde{O}(A_{\text{tot}}[(1 - \gamma)^{-3}\epsilon^{-2} + (1 - \gamma)^{-3}])$ time [Sidford, Wang, Wu, Ye 2018] in the sampling setting, $\tilde{O}(s + A_{\text{tot}} (1-\gamma)^{-3})$ time [Sidford, Wang, Wu, Yang, Ye 2018] in the offline setting, or time at least quadratic in the number of states using interior point methods for linear programming. We achieve our results by building upon prior stochastic variance-reduced value iteration methods [Sidford, Wang, Wu, Yang, Ye 2018]. We provide a variant that carefully truncates the progress of its iterates to improve the variance of new variance-reduced sampling procedures that we introduce to implement the steps. Our method is essentially model-free and can be implemented in $\tilde{O}(A_{\text{tot}})$-space when given generative model access. Consequently, our results take a step in closing the sample-complexity gap between model-free and model-based methods.

A Whole New Ball Game: A Primal Accelerated Method for Matrix Games and Minimizing the Maximum of Smooth Functions

We design algorithms for minimizing $\max_{i\in[n]} f_i(x)$ over a $d$-dimensional Euclidean or simplex domain. When each $f_i$ is $1$-Lipschitz and $1$-smooth, our method computes an $\epsilon$-approximate solution using $\widetilde{O}(n \epsilon^{-1/3} + \epsilon^{-2})$ gradient and function evaluations, and $\widetilde{O}(n \epsilon^{-4/3})$ additional runtime. For large $n$, our evaluation complexity is optimal up to polylogarithmic factors. In the special case where each $f_i$ is linear -- which corresponds to finding a near-optimal primal strategy in a matrix game -- our method finds an $\epsilon$-approximate solution in runtime $\widetilde{O}(n (d/\epsilon)^{2/3} + nd + d\epsilon^{-2})$. For $n>d$ and $\epsilon=1/\sqrt{n}$ this improves over all existing first-order methods. When additionally $d = \omega(n^{8/11})$ our runtime also improves over all known interior point methods. Our algorithm combines three novel primitives: (1) A dynamic data structure which enables efficient stochastic gradient estimation in small $\ell_2$ or $\ell_1$ balls. (2) A mirror descent algorithm tailored to our data structure implementing an oracle which minimizes the objective over these balls. (3) A simple ball oracle acceleration framework suitable for non-Euclidean geometry.

Moments, Random Walks, and Limits for Spectrum Approximation

We study lower bounds for the problem of approximating a one dimensional distribution given (noisy) measurements of its moments. We show that there are distributions on $[-1,1]$ that cannot be approximated to accuracy $\epsilon$ in Wasserstein-1 distance even if we know \emph{all} of their moments to multiplicative accuracy $(1\pm2^{-\Omega(1/\epsilon)})$; this result matches an upper bound of Kong and Valiant [Annals of Statistics, 2017]. To obtain our result, we provide a hard instance involving distributions induced by the eigenvalue spectra of carefully constructed graph adjacency matrices. Efficiently approximating such spectra in Wasserstein-1 distance is a well-studied algorithmic problem, and a recent result of Cohen-Steiner et al. [KDD 2018] gives a method based on accurately approximating spectral moments using $2^{O(1/\epsilon)}$ random walks initiated at uniformly random nodes in the graph. As a strengthening of our main result, we show that improving the dependence on $1/\epsilon$ in this result would require a new algorithmic approach. Specifically, no algorithm can compute an $\epsilon$-accurate approximation to the spectrum of a normalized graph adjacency matrix with constant probability, even when given the transcript of $2^{\Omega(1/\epsilon)}$ random walks of length $2^{\Omega(1/\epsilon)}$ started at random nodes.

ReSQueing Parallel and Private Stochastic Convex Optimization

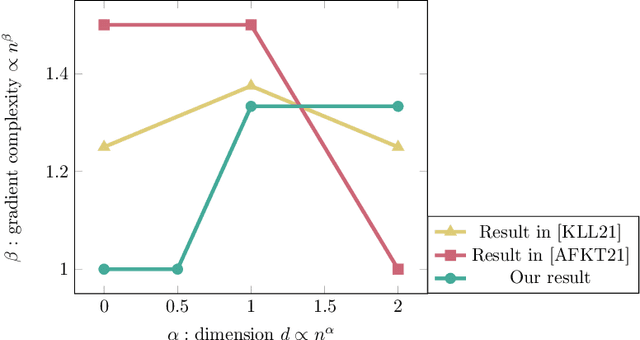
We introduce a new tool for stochastic convex optimization (SCO): a Reweighted Stochastic Query (ReSQue) estimator for the gradient of a function convolved with a (Gaussian) probability density. Combining ReSQue with recent advances in ball oracle acceleration [CJJJLST20, ACJJS21], we develop algorithms achieving state-of-the-art complexities for SCO in parallel and private settings. For a SCO objective constrained to the unit ball in $\mathbb{R}^d$, we obtain the following results (up to polylogarithmic factors). We give a parallel algorithm obtaining optimization error $\epsilon_{\text{opt}}$ with $d^{1/3}\epsilon_{\text{opt}}^{-2/3}$ gradient oracle query depth and $d^{1/3}\epsilon_{\text{opt}}^{-2/3} + \epsilon_{\text{opt}}^{-2}$ gradient queries in total, assuming access to a bounded-variance stochastic gradient estimator. For $\epsilon_{\text{opt}} \in [d^{-1}, d^{-1/4}]$, our algorithm matches the state-of-the-art oracle depth of [BJLLS19] while maintaining the optimal total work of stochastic gradient descent. We give an $(\epsilon_{\text{dp}}, \delta)$-differentially private algorithm which, given $n$ samples of Lipschitz loss functions, obtains near-optimal optimization error and makes $\min(n, n^2\epsilon_{\text{dp}}^2 d^{-1}) + \min(n^{4/3}\epsilon_{\text{dp}}^{1/3}, (nd)^{2/3}\epsilon_{\text{dp}}^{-1})$ queries to the gradients of these functions. In the regime $d \le n \epsilon_{\text{dp}}^{2}$, where privacy comes at no cost in terms of the optimal loss up to constants, our algorithm uses $n + (nd)^{2/3}\epsilon_{\text{dp}}^{-1}$ queries and improves recent advancements of [KLL21, AFKT21]. In the moderately low-dimensional setting $d \le \sqrt n \epsilon_{\text{dp}}^{3/2}$, our query complexity is near-linear.

VO$Q$L: Towards Optimal Regret in Model-free RL with Nonlinear Function Approximation

We study time-inhomogeneous episodic reinforcement learning (RL) under general function approximation and sparse rewards. We design a new algorithm, Variance-weighted Optimistic $Q$-Learning (VO$Q$L), based on $Q$-learning and bound its regret assuming completeness and bounded Eluder dimension for the regression function class. As a special case, VO$Q$L achieves $\tilde{O}(d\sqrt{HT}+d^6H^{5})$ regret over $T$ episodes for a horizon $H$ MDP under ($d$-dimensional) linear function approximation, which is asymptotically optimal. Our algorithm incorporates weighted regression-based upper and lower bounds on the optimal value function to obtain this improved regret. The algorithm is computationally efficient given a regression oracle over the function class, making this the first computationally tractable and statistically optimal approach for linear MDPs.

RECAPP: Crafting a More Efficient Catalyst for Convex Optimization

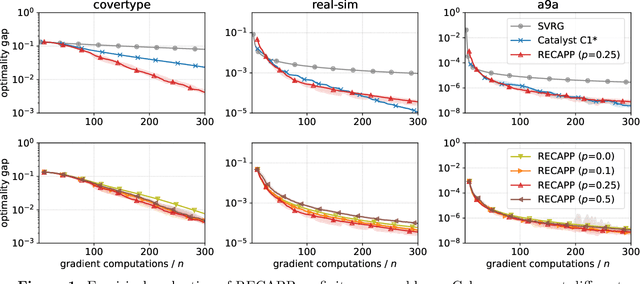
The accelerated proximal point algorithm (APPA), also known as "Catalyst", is a well-established reduction from convex optimization to approximate proximal point computation (i.e., regularized minimization). This reduction is conceptually elegant and yields strong convergence rate guarantees. However, these rates feature an extraneous logarithmic term arising from the need to compute each proximal point to high accuracy. In this work, we propose a novel Relaxed Error Criterion for Accelerated Proximal Point (RECAPP) that eliminates the need for high accuracy subproblem solutions. We apply RECAPP to two canonical problems: finite-sum and max-structured minimization. For finite-sum problems, we match the best known complexity, previously obtained by carefully-designed problem-specific algorithms. For minimizing $\max_y f(x,y)$ where $f$ is convex in $x$ and strongly-concave in $y$, we improve on the best known (Catalyst-based) bound by a logarithmic factor.

Sharper Rates for Separable Minimax and Finite Sum Optimization via Primal-Dual Extragradient Methods

We design accelerated algorithms with improved rates for several fundamental classes of optimization problems. Our algorithms all build upon techniques related to the analysis of primal-dual extragradient methods via relative Lipschitzness proposed recently by [CST21]. (1) Separable minimax optimization. We study separable minimax optimization problems $\min_x \max_y f(x) - g(y) + h(x, y)$, where $f$ and $g$ have smoothness and strong convexity parameters $(L^x, \mu^x)$, $(L^y, \mu^y)$, and $h$ is convex-concave with a $(\Lambda^{xx}, \Lambda^{xy}, \Lambda^{yy})$-blockwise operator norm bounded Hessian. We provide an algorithm with gradient query complexity $\tilde{O}\left(\sqrt{\frac{L^{x}}{\mu^{x}}} + \sqrt{\frac{L^{y}}{\mu^{y}}} + \frac{\Lambda^{xx}}{\mu^{x}} + \frac{\Lambda^{xy}}{\sqrt{\mu^{x}\mu^{y}}} + \frac{\Lambda^{yy}}{\mu^{y}}\right)$. Notably, for convex-concave minimax problems with bilinear coupling (e.g.\ quadratics), where $\Lambda^{xx} = \Lambda^{yy} = 0$, our rate matches a lower bound of [ZHZ19]. (2) Finite sum optimization. We study finite sum optimization problems $\min_x \frac{1}{n}\sum_{i\in[n]} f_i(x)$, where each $f_i$ is $L_i$-smooth and the overall problem is $\mu$-strongly convex. We provide an algorithm with gradient query complexity $\tilde{O}\left(n + \sum_{i\in[n]} \sqrt{\frac{L_i}{n\mu}} \right)$. Notably, when the smoothness bounds $\{L_i\}_{i\in[n]}$ are non-uniform, our rate improves upon accelerated SVRG [LMH15, FGKS15] and Katyusha [All17] by up to a $\sqrt{n}$ factor. (3) Minimax finite sums. We generalize our algorithms for minimax and finite sum optimization to solve a natural family of minimax finite sum optimization problems at an accelerated rate, encapsulating both above results up to a logarithmic factor.

A Unified Framework for Multi-distribution Density Ratio Estimation

Binary density ratio estimation (DRE), the problem of estimating the ratio $p_1/p_2$ given their empirical samples, provides the foundation for many state-of-the-art machine learning algorithms such as contrastive representation learning and covariate shift adaptation. In this work, we consider a generalized setting where given samples from multiple distributions $p_1, \ldots, p_k$ (for $k > 2$), we aim to efficiently estimate the density ratios between all pairs of distributions. Such a generalization leads to important new applications such as estimating statistical discrepancy among multiple random variables like multi-distribution $f$-divergence, and bias correction via multiple importance sampling. We then develop a general framework from the perspective of Bregman divergence minimization, where each strictly convex multivariate function induces a proper loss for multi-distribution DRE. Moreover, we rederive the theoretical connection between multi-distribution density ratio estimation and class probability estimation, justifying the use of any strictly proper scoring rule composite with a link function for multi-distribution DRE. We show that our framework leads to methods that strictly generalize their counterparts in binary DRE, as well as new methods that show comparable or superior performance on various downstream tasks.