Distance Adaptive Beam Search for Provably Accurate Graph-Based Nearest Neighbor Search

Nearest neighbor search is central in machine learning, information retrieval, and databases. For high-dimensional datasets, graph-based methods such as HNSW, DiskANN, and NSG have become popular thanks to their empirical accuracy and efficiency. These methods construct a directed graph over the dataset and perform beam search on the graph to find nodes close to a given query. While significant work has focused on practical refinements and theoretical understanding of graph-based methods, many questions remain. We propose a new distance-based termination condition for beam search to replace the commonly used condition based on beam width. We prove that, as long as the search graph is navigable, our resulting Adaptive Beam Search method is guaranteed to approximately solve the nearest-neighbor problem, establishing a connection between navigability and the performance of graph-based search. We also provide extensive experiments on our new termination condition for both navigable graphs and approximately navigable graphs used in practice, such as HNSW and Vamana graphs. We find that Adaptive Beam Search outperforms standard beam search over a range of recall values, data sets, graph constructions, and target number of nearest neighbors. It thus provides a simple and practical way to improve the performance of popular methods.

Beyond Quantile Methods: Improved Top-K Threshold Estimation for Traditional and Learned Sparse Indexes

Top-k threshold estimation is the problem of estimating the score of the k-th highest ranking result of a search query. A good estimate can be used to speed up many common top-k query processing algorithms, and thus a number of researchers have recently studied the problem. Among the various approaches that have been proposed, quantile methods appear to give the best estimates overall at modest computational costs, followed by sampling-based methods in certain cases. In this paper, we make two main contributions. First, we study how to get even better estimates than the state of the art. Starting from quantile-based methods, we propose a series of enhancements that give improved estimates in terms of the commonly used mean under-prediction fraction (MUF). Second, we study the threshold estimation problem on recently proposed learned sparse index structures, showing that our methods also work well for these cases. Our best methods substantially narrow the gap between the state of the art and the ideal MUF of 1.0, at some additional cost in time and space.

Navigable Graphs for High-Dimensional Nearest Neighbor Search: Constructions and Limits

There has been significant recent interest in graph-based nearest neighbor search methods, many of which are centered on the construction of navigable graphs over high-dimensional point sets. A graph is navigable if we can successfully move from any starting node to any target node using a greedy routing strategy where we always move to the neighbor that is closest to the destination according to a given distance function. The complete graph is navigable for any point set, but the important question for applications is if sparser graphs can be constructed. While this question is fairly well understood in low-dimensions, we establish some of the first upper and lower bounds for high-dimensional point sets. First, we give a simple and efficient way to construct a navigable graph with average degree $O(\sqrt{n \log n })$ for any set of $n$ points, in any dimension, for any distance function. We compliment this result with a nearly matching lower bound: even under the Euclidean metric in $O(\log n)$ dimensions, a random point set has no navigable graph with average degree $O(n^{\alpha})$ for any $\alpha < 1/2$. Our lower bound relies on sharp anti-concentration bounds for binomial random variables, which we use to show that the near-neighborhoods of a set of random points do not overlap significantly, forcing any navigable graph to have many edges.

Realtime Mobile Bandwidth and Handoff Predictions in 4G/5G Networks

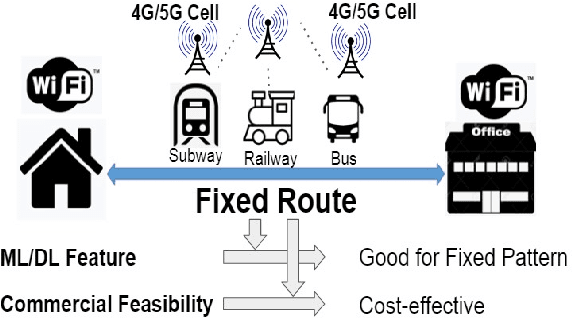
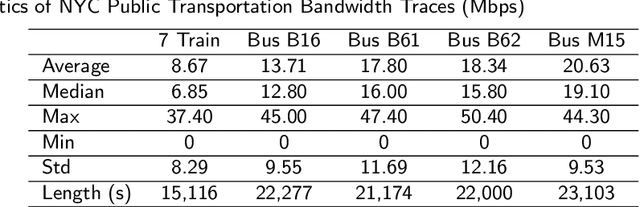
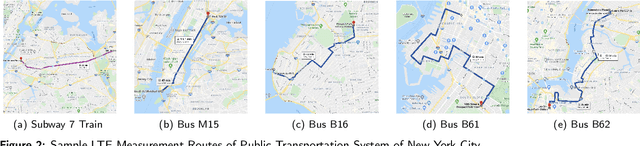
Mobile apps are increasingly relying on high-throughput and low-latency content delivery, while the available bandwidth on wireless access links is inherently time-varying. The handoffs between base stations and access modes due to user mobility present additional challenges to deliver a high level of user Quality-of-Experience (QoE). The ability to predict the available bandwidth and the upcoming handoffs will give applications valuable leeway to make proactive adjustments to avoid significant QoE degradation. In this paper, we explore the possibility and accuracy of realtime mobile bandwidth and handoff predictions in 4G/LTE and 5G networks. Towards this goal, we collect long consecutive traces with rich bandwidth, channel, and context information from public transportation systems. We develop Recurrent Neural Network models to mine the temporal patterns of bandwidth evolution in fixed-route mobility scenarios. Our models consistently outperform the conventional univariate and multivariate bandwidth prediction models. For 4G \& 5G co-existing networks, we propose a new problem of handoff prediction between 4G and 5G, which is important for low-latency applications like self-driving strategy in realistic 5G scenarios. We develop classification and regression based prediction models, which achieve more than 80\% accuracy in predicting 4G and 5G handoffs in a recent 5G dataset.