No-regret Algorithms for Fair Resource Allocation
Paper and Code
Mar 11, 2023
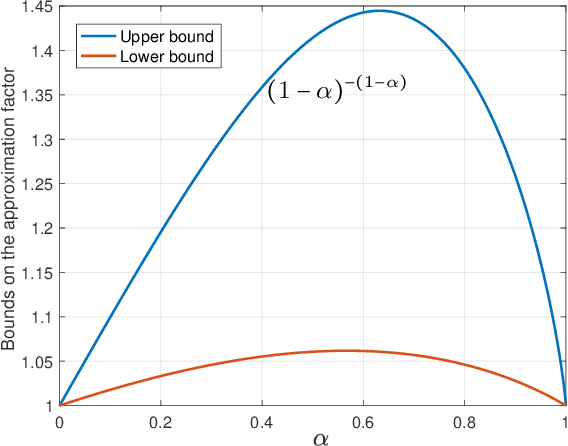

We consider a fair resource allocation problem in the no-regret setting against an unrestricted adversary. The objective is to allocate resources equitably among several agents in an online fashion so that the difference of the aggregate $\alpha$-fair utilities of the agents between an optimal static clairvoyant allocation and that of the online policy grows sub-linearly with time. The problem is challenging due to the non-additive nature of the $\alpha$-fairness function. Previously, it was shown that no online policy can exist for this problem with a sublinear standard regret. In this paper, we propose an efficient online resource allocation policy, called Online Proportional Fair (OPF), that achieves $c_\alpha$-approximate sublinear regret with the approximation factor $c_\alpha=(1-\alpha)^{-(1-\alpha)}\leq 1.445,$ for $0\leq \alpha < 1$. The upper bound to the $c_\alpha$-regret for this problem exhibits a surprising phase transition phenomenon. The regret bound changes from a power-law to a constant at the critical exponent $\alpha=\frac{1}{2}.$ As a corollary, our result also resolves an open problem raised by Even-Dar et al. [2009] on designing an efficient no-regret policy for the online job scheduling problem in certain parameter regimes. The proof of our results introduces new algorithmic and analytical techniques, including greedy estimation of the future gradients for non-additive global reward functions and bootstrapping adaptive regret bounds, which may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge