Fast and Reliable $N-k$ Contingency Screening with Input-Convex Neural Networks

Power system operators must ensure that dispatch decisions remain feasible in case of grid outages or contingencies to prevent cascading failures and ensure reliable operation. However, checking the feasibility of all $N - k$ contingencies -- every possible simultaneous failure of $k$ grid components -- is computationally intractable for even small $k$, requiring system operators to resort to heuristic screening methods. Because of the increase in uncertainty and changes in system behaviors, heuristic lists might not include all relevant contingencies, generating false negatives in which unsafe scenarios are misclassified as safe. In this work, we propose to use input-convex neural networks (ICNNs) for contingency screening. We show that ICNN reliability can be determined by solving a convex optimization problem, and by scaling model weights using this problem as a differentiable optimization layer during training, we can learn an ICNN classifier that is both data-driven and has provably guaranteed reliability. Namely, our method can ensure a zero false negative rate. We empirically validate this methodology in a case study on the IEEE 39-bus test network, observing that it yields substantial (10-20x) speedups while having excellent classification accuracy.

End-to-End Conformal Calibration for Optimization Under Uncertainty

Machine learning can significantly improve performance for decision-making under uncertainty in a wide range of domains. However, ensuring robustness guarantees requires well-calibrated uncertainty estimates, which can be difficult to achieve in high-capacity prediction models such as deep neural networks. Moreover, in high-dimensional settings, there may be many valid uncertainty estimates, each with their own performance profile - i.e., not all uncertainty is equally valuable for downstream decision-making. To address this problem, this paper develops an end-to-end framework to learn the uncertainty estimates for conditional robust optimization, with robustness and calibration guarantees provided by conformal prediction. In addition, we propose to represent arbitrary convex uncertainty sets with partially input-convex neural networks, which are learned as part of our framework. Our approach consistently improves upon two-stage estimate-then-optimize baselines on concrete applications in energy storage arbitrage and portfolio optimization.

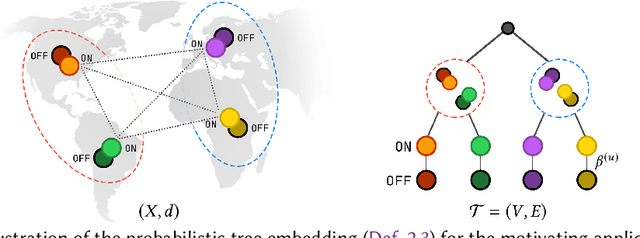
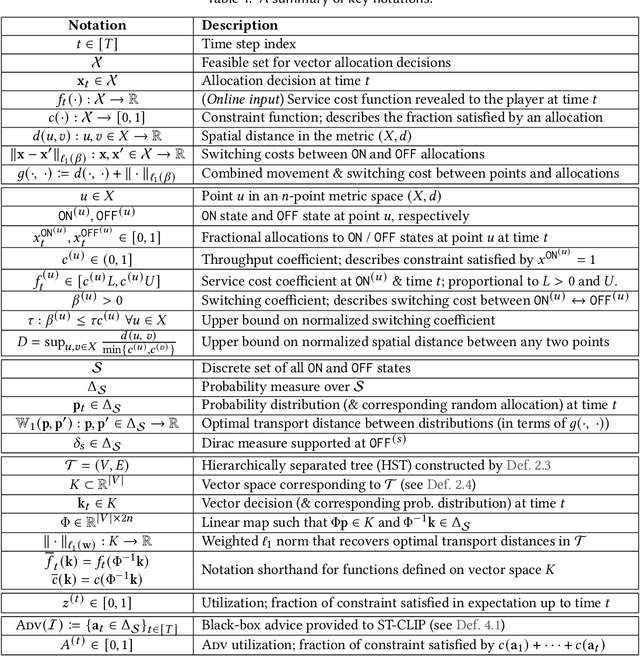
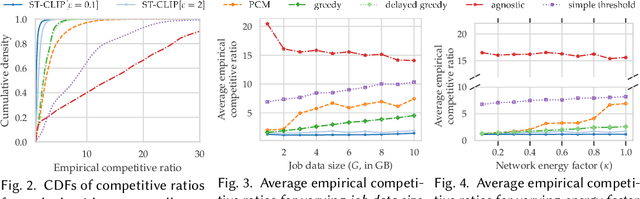
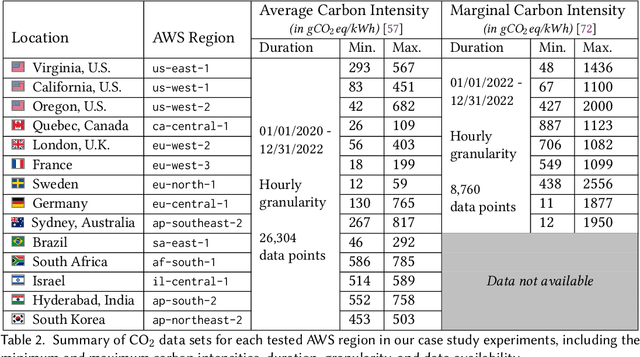
CarbonClipper: Optimal Algorithms for Carbon-Aware Spatiotemporal Workload Management

We study carbon-aware spatiotemporal workload management, which seeks to address the growing environmental impact of data centers. We formalize this as an online problem called spatiotemporal online allocation with deadline constraints ($\mathsf{SOAD}$), in which an online player completes a workload (e.g., a batch compute job) by moving and scheduling the workload across a network subject to a deadline $T$. At each time step, a service cost function is revealed, representing, e.g., the carbon intensity of servicing a workload at each location, and the player must irrevocably decide the current allocation. Furthermore, whenever the player moves the allocation, it incurs a movement cost defined by a metric space $(X,d)$ that captures, e.g., the overhead of migrating a compute job. $\mathsf{SOAD}$ formalizes the open problem of combining general metrics and deadline constraints in the online algorithms literature, unifying problems such as metrical task systems and online search. We propose a competitive algorithm for $\mathsf{SOAD}$ along with a matching lower bound that proves it is optimal. Our main algorithm, ${\rm C{\scriptsize ARBON}C{\scriptsize LIPPER}}$, is a learning-augmented algorithm that takes advantage of predictions (e.g., carbon intensity forecasts) and achieves an optimal consistency-robustness trade-off. We evaluate our proposed algorithms for carbon-aware spatiotemporal workload management on a simulated global data center network, showing that ${\rm C{\scriptsize ARBON}C{\scriptsize LIPPER}}$ significantly improves performance compared to baseline methods and delivers meaningful carbon reductions.

Chasing Convex Functions with Long-term Constraints

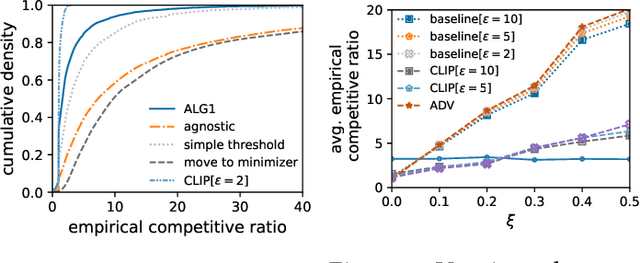
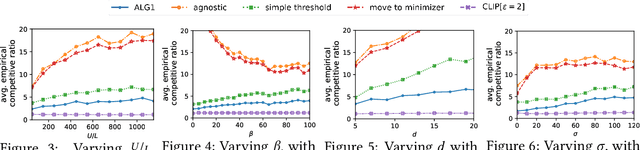
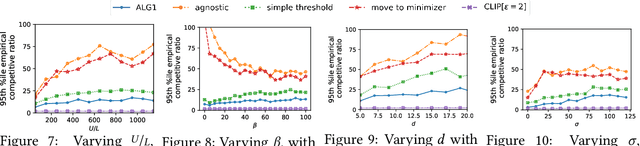
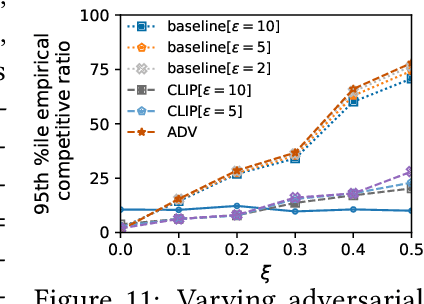
We introduce and study a family of online metric problems with long-term constraints. In these problems, an online player makes decisions $\mathbf{x}_t$ in a metric space $(X,d)$ to simultaneously minimize their hitting cost $f_t(\mathbf{x}_t)$ and switching cost as determined by the metric. Over the time horizon $T$, the player must satisfy a long-term demand constraint $\sum_{t} c(\mathbf{x}_t) \geq 1$, where $c(\mathbf{x}_t)$ denotes the fraction of demand satisfied at time $t$. Such problems can find a wide array of applications to online resource allocation in sustainable energy and computing systems. We devise optimal competitive and learning-augmented algorithms for specific instantiations of these problems, and further show that our proposed algorithms perform well in numerical experiments.

Online Conversion with Switching Costs: Robust and Learning-Augmented Algorithms

We introduce and study online conversion with switching costs, a family of online problems that capture emerging problems at the intersection of energy and sustainability. In this problem, an online player attempts to purchase (alternatively, sell) fractional shares of an asset during a fixed time horizon with length $T$. At each time step, a cost function (alternatively, price function) is revealed, and the player must irrevocably decide an amount of asset to convert. The player also incurs a switching cost whenever their decision changes in consecutive time steps, i.e., when they increase or decrease their purchasing amount. We introduce competitive (robust) threshold-based algorithms for both the minimization and maximization variants of this problem, and show they are optimal among deterministic online algorithms. We then propose learning-augmented algorithms that take advantage of untrusted black-box advice (such as predictions from a machine learning model) to achieve significantly better average-case performance without sacrificing worst-case competitive guarantees. Finally, we empirically evaluate our proposed algorithms using a carbon-aware EV charging case study, showing that our algorithms substantially improve on baseline methods for this problem.

Online Algorithms with Uncertainty-Quantified Predictions

Online algorithms with predictions have become a trending topic in the field of beyond worst-case analysis of algorithms. These algorithms incorporate predictions about the future to obtain performance guarantees that are of high quality when the predictions are good, while still maintaining bounded worst-case guarantees when predictions are arbitrarily poor. In general, the algorithm is assumed to be unaware of the prediction's quality. However, recent developments in the machine learning literature have studied techniques for providing uncertainty quantification on machine-learned predictions, which describes how certain a model is about its quality. This paper examines the question of how to optimally utilize uncertainty-quantified predictions in the design of online algorithms. In particular, we consider predictions augmented with uncertainty quantification describing the likelihood of the ground truth falling in a certain range, designing online algorithms with these probabilistic predictions for two classic online problems: ski rental and online search. In each case, we demonstrate that non-trivial modifications to algorithm design are needed to fully leverage the probabilistic predictions. Moreover, we consider how to utilize more general forms of uncertainty quantification, proposing a framework based on online learning that learns to exploit uncertainty quantification to make optimal decisions in multi-instance settings.

Chasing Convex Bodies and Functions with Black-Box Advice

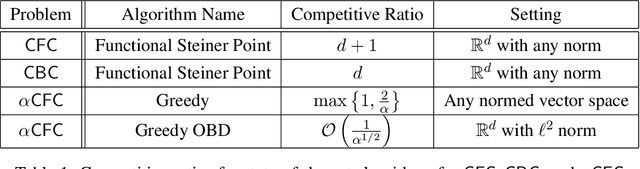
We consider the problem of convex function chasing with black-box advice, where an online decision-maker aims to minimize the total cost of making and switching between decisions in a normed vector space, aided by black-box advice such as the decisions of a machine-learned algorithm. The decision-maker seeks cost comparable to the advice when it performs well, known as $\textit{consistency}$, while also ensuring worst-case $\textit{robustness}$ even when the advice is adversarial. We first consider the common paradigm of algorithms that switch between the decisions of the advice and a competitive algorithm, showing that no algorithm in this class can improve upon 3-consistency while staying robust. We then propose two novel algorithms that bypass this limitation by exploiting the problem's convexity. The first, INTERP, achieves $(\sqrt{2}+\epsilon)$-consistency and $\mathcal{O}(\frac{C}{\epsilon^2})$-robustness for any $\epsilon > 0$, where $C$ is the competitive ratio of an algorithm for convex function chasing or a subclass thereof. The second, BDINTERP, achieves $(1+\epsilon)$-consistency and $\mathcal{O}(\frac{CD}{\epsilon})$-robustness when the problem has bounded diameter $D$. Further, we show that BDINTERP achieves near-optimal consistency-robustness trade-off for the special case where cost functions are $\alpha$-polyhedral.