Fast and Reliable $N-k$ Contingency Screening with Input-Convex Neural Networks

Power system operators must ensure that dispatch decisions remain feasible in case of grid outages or contingencies to prevent cascading failures and ensure reliable operation. However, checking the feasibility of all $N - k$ contingencies -- every possible simultaneous failure of $k$ grid components -- is computationally intractable for even small $k$, requiring system operators to resort to heuristic screening methods. Because of the increase in uncertainty and changes in system behaviors, heuristic lists might not include all relevant contingencies, generating false negatives in which unsafe scenarios are misclassified as safe. In this work, we propose to use input-convex neural networks (ICNNs) for contingency screening. We show that ICNN reliability can be determined by solving a convex optimization problem, and by scaling model weights using this problem as a differentiable optimization layer during training, we can learn an ICNN classifier that is both data-driven and has provably guaranteed reliability. Namely, our method can ensure a zero false negative rate. We empirically validate this methodology in a case study on the IEEE 39-bus test network, observing that it yields substantial (10-20x) speedups while having excellent classification accuracy.

An Efficient Learning-Based Solver for Two-Stage DC Optimal Power Flow with Feasibility Guarantees

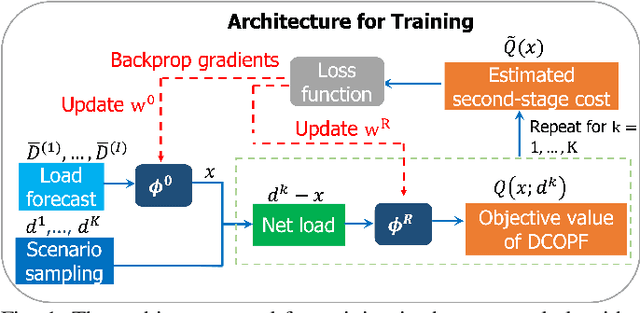
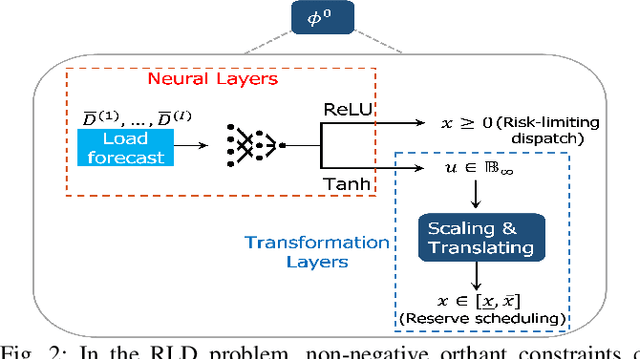
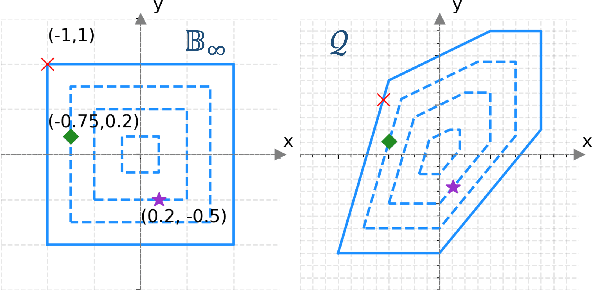
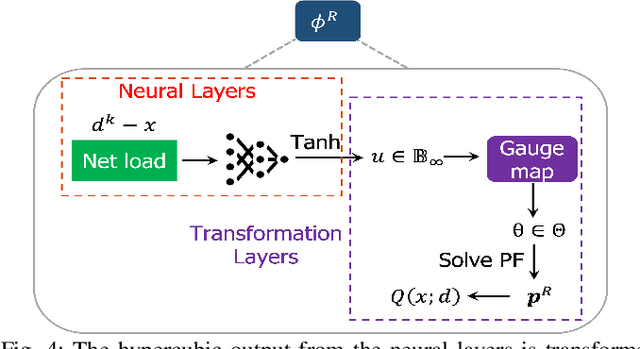
In this paper, we consider the scenario-based two-stage stochastic DC optimal power flow (OPF) problem for optimal and reliable dispatch when the load is facing uncertainty. Although this problem is a linear program, it remains computationally challenging to solve due to the large number of scenarios needed to accurately represent the uncertainties. To mitigate the computational issues, many techniques have been proposed to approximate the second-stage decisions so they can dealt more efficiently. The challenge of finding good policies to approximate the second-stage decisions is that these solutions need to be feasible, which has been difficult to achieve with existing policies. To address these challenges, this paper proposes a learning method to solve the two-stage problem in a more efficient and optimal way. A technique called the gauge map is incorporated into the learning architecture design to guarantee the learned solutions' feasibility to the network constraints. Namely, we can design policies that are feed forward functions that only output feasible solutions. Simulation results on standard IEEE systems show that, compared to iterative solvers and the widely used affine policy, our proposed method not only learns solutions of good quality but also accelerates the computation by orders of magnitude.

Solving Differential-Algebraic Equations in Power Systems Dynamics with Neural Networks and Spatial Decomposition

The dynamics of the power system are described by a system of differential-algebraic equations. Time-domain simulations are used to understand the evolution of the system dynamics. These simulations can be computationally expensive due to the stiffness of the system which requires the use of finely discretized time-steps. By increasing the allowable time-step size, we aim to accelerate such simulations. In this paper, we use the observation that even though the individual components are described using both algebraic and differential equations, their coupling only involves algebraic equations. Following this observation, we use Neural Networks (NNs) to approximate the components' state evolution, leading to fast, accurate, and numerically stable approximators, which enable larger time-steps. To account for effects of the network on the components and vice-versa, the NNs take the temporal evolution of the coupling algebraic variables as an input for their prediction. We initially estimate this temporal evolution and then update it in an iterative fashion using the Newton-Raphson algorithm. The involved Jacobian matrix is calculated with Automatic Differentiation and its size depends only on the network size but not on the component dynamics. We demonstrate this NN-based simulator on the IEEE 9-bus test case with 3 generators.

Interpreting Primal-Dual Algorithms for Constrained MARL

Constrained multiagent reinforcement learning (C-MARL) is gaining importance as MARL algorithms find new applications in real-world systems ranging from energy systems to drone swarms. Most C-MARL algorithms use a primal-dual approach to enforce constraints through a penalty function added to the reward. In this paper, we study the structural effects of this penalty term on the MARL problem. First, we show that the standard practice of using the constraint function as the penalty leads to a weak notion of safety. However, by making simple modifications to the penalty term, we can enforce meaningful probabilistic (chance and conditional value at risk) constraints. Second, we quantify the effect of the penalty term on the value function, uncovering an improved value estimation procedure. We use these insights to propose a constrained multiagent advantage actor critic (C-MAA2C) algorithm. Simulations in a simple constrained multiagent environment affirm that our reinterpretation of the primal-dual method in terms of probabilistic constraints is effective, and that our proposed value estimate accelerates convergence to a safe joint policy.

Efficient Reinforcement Learning Through Trajectory Generation

A key barrier to using reinforcement learning (RL) in many real-world applications is the requirement of a large number of system interactions to learn a good control policy. Off-policy and Offline RL methods have been proposed to reduce the number of interactions with the physical environment by learning control policies from historical data. However, their performances suffer from the lack of exploration and the distributional shifts in trajectories once controllers are updated. Moreover, most RL methods require that all states are directly observed, which is difficult to be attained in many settings. To overcome these challenges, we propose a trajectory generation algorithm, which adaptively generates new trajectories as if the system is being operated and explored under the updated control policies. Motivated by the fundamental lemma for linear systems, assuming sufficient excitation, we generate trajectories from linear combinations of historical trajectories. For linear feedback control, we prove that the algorithm generates trajectories with the exact distribution as if they are sampled from the real system using the updated control policy. In particular, the algorithm extends to systems where the states are not directly observed. Experiments show that the proposed method significantly reduces the number of sampled data needed for RL algorithms.

Learning to Solve the AC Optimal Power Flow via a Lagrangian Approach

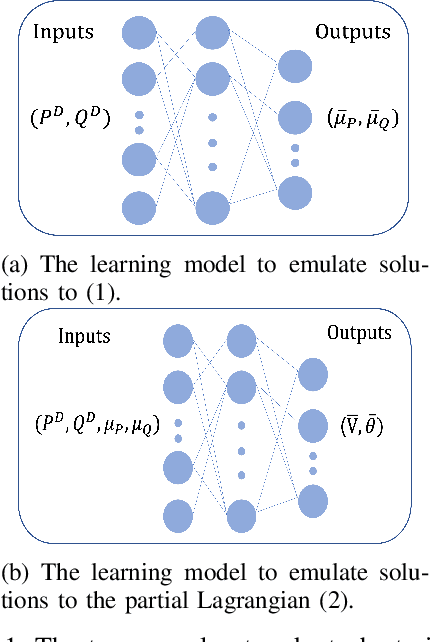
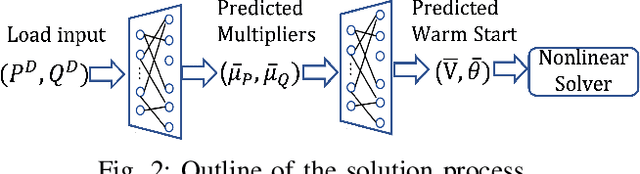
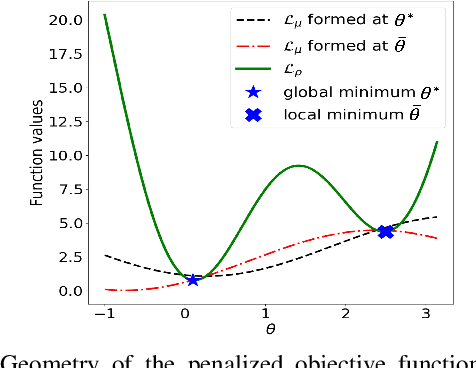
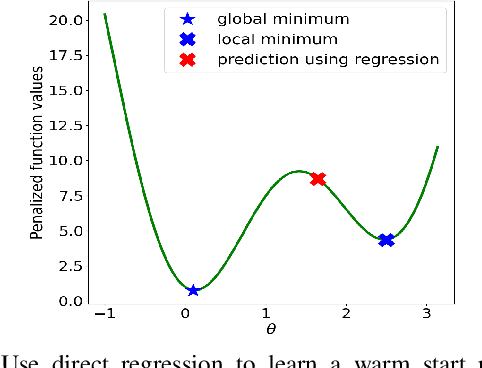
Using deep neural networks to predict the solutions of AC optimal power flow (ACOPF) problems has been an active direction of research. However, because the ACOPF is nonconvex, it is difficult to construct a good data set that contains mostly globally optimal solutions. To overcome the challenge that the training data may contain suboptimal solutions, we propose a Lagrangian-based approach. First, we use a neural network to learn the dual variables of the ACOPF problem. Then we use a second neural network to predict solutions of the partial Lagrangian from the predicted dual variables. Since the partial Lagrangian has a much better optimization landscape, we use the predicted solutions from the neural network as a warm start for the ACOPF problem. Using standard and modified IEEE 22-bus, 39-bus, and 118-bus networks, we show that our approach is able to obtain the globally optimal cost even when the training data is mostly comprised of suboptimal solutions.

Lyapunov-Regularized Reinforcement Learning for Power System Transient Stability

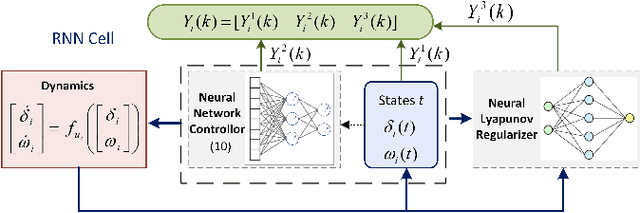
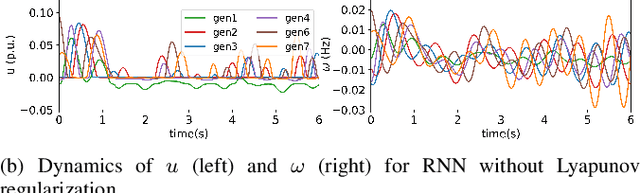
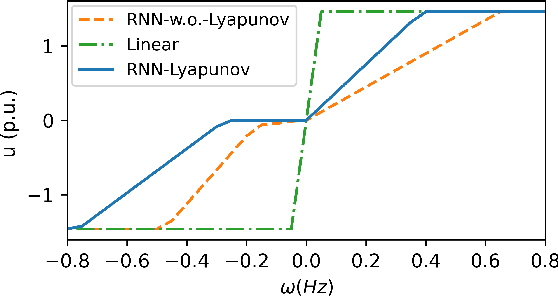
Transient stability of power systems is becoming increasingly important because of the growing integration of renewable resources. These resources lead to a reduction in mechanical inertia but also provide increased flexibility in frequency responses. Namely, their power electronic interfaces can implement almost arbitrary control laws. To design these controllers, reinforcement learning (RL) has emerged as a powerful method in searching for optimal non-linear control policy parameterized by neural networks. A key challenge is to enforce that a learned controller must be stabilizing. This paper proposes a Lyapunov regularized RL approach for optimal frequency control for transient stability in lossy networks. Because the lack of an analytical Lyapunov function, we learn a Lyapunov function parameterized by a neural network. The losses are specially designed with respect to the physical power system. The learned neural Lyapunov function is then utilized as a regularization to train the neural network controller by penalizing actions that violate the Lyapunov conditions. Case study shows that introducing the Lyapunov regularization enables the controller to be stabilizing and achieve smaller losses.

Multi-Agent Reinforcement Learning in Cournot Games

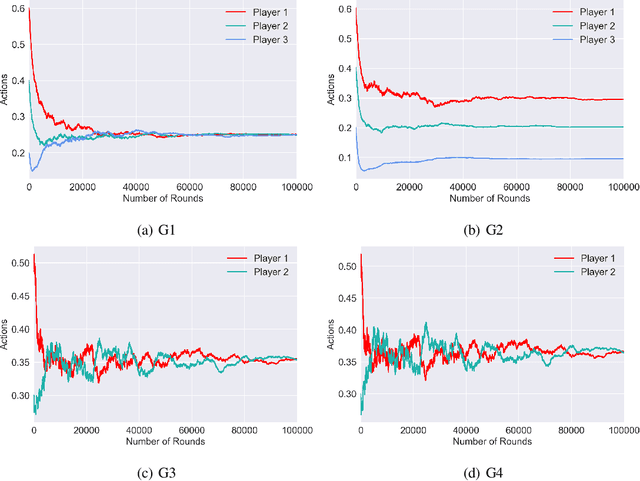
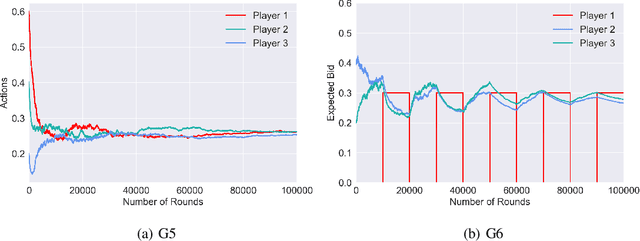
In this work, we study the interaction of strategic agents in continuous action Cournot games with limited information feedback. Cournot game is the essential market model for many socio-economic systems where agents learn and compete without the full knowledge of the system or each other. We consider the dynamics of the policy gradient algorithm, which is a widely adopted continuous control reinforcement learning algorithm, in concave Cournot games. We prove the convergence of policy gradient dynamics to the Nash equilibrium when the price function is linear or the number of agents is two. This is the first result (to the best of our knowledge) on the convergence property of learning algorithms with continuous action spaces that do not fall in the no-regret class.

Safe Reinforcement Learning of Control-Affine Systems with Vertex Networks

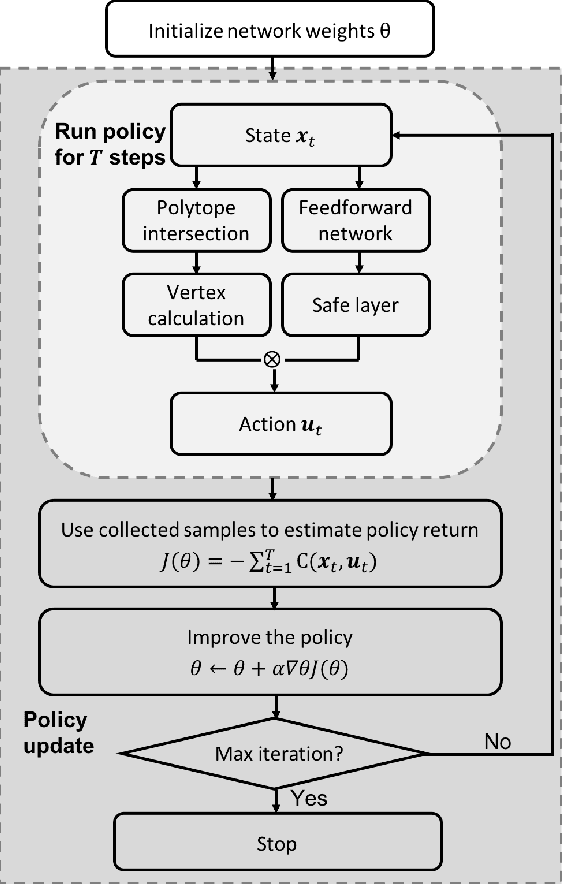
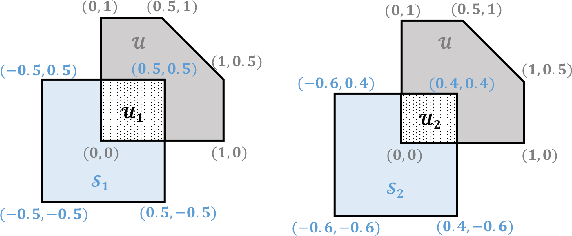
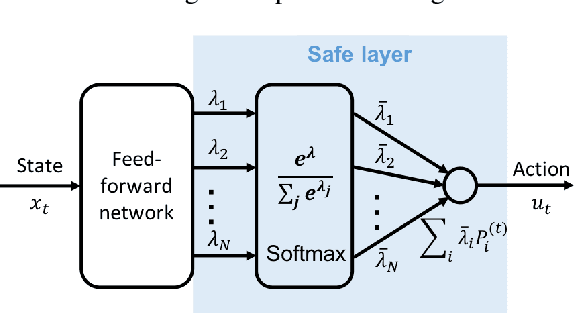
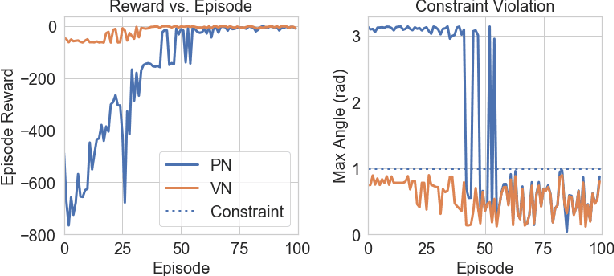
This paper focuses on finding reinforcement learning policies for control systems with hard state and action constraints. Despite its success in many domains, reinforcement learning is challenging to apply to problems with hard constraints, especially if both the state variables and actions are constrained. Previous works seeking to ensure constraint satisfaction, or safety, have focused on adding a projection step to a learned policy. Yet, this approach requires solving an optimization problem at every policy execution step, which can lead to significant computational costs. To tackle this problem, this paper proposes a new approach, termed Vertex Networks (VNs), with guarantees on safety during exploration and on learned control policies by incorporating the safety constraints into the policy network architecture. Leveraging the geometric property that all points within a convex set can be represented as the convex combination of its vertices, the proposed algorithm first learns the convex combination weights and then uses these weights along with the pre-calculated vertices to output an action. The output action is guaranteed to be safe by construction. Numerical examples illustrate that the proposed VN algorithm outperforms vanilla reinforcement learning in a variety of benchmark control tasks.

Transfer Learning for HVAC System Fault Detection

Faults in HVAC systems degrade thermal comfort and energy efficiency in buildings and have received significant attention from the research community, with data driven methods gaining in popularity. Yet the lack of labeled data, such as normal versus faulty operational status, has slowed the application of machine learning to HVAC systems. In addition, for any particular building, there may be an insufficient number of observed faults over a reasonable amount of time for training. To overcome these challenges, we present a transfer methodology for a novel Bayesian classifier designed to distinguish between normal operations and faulty operations. The key is to train this classifier on a building with a large amount of sensor and fault data (for example, via simulation or standard test data) then transfer the classifier to a new building using a small amount of normal operations data from the new building. We demonstrate a proof-of-concept for transferring a classifier between architecturally similar buildings in different climates and show few samples are required to maintain classification precision and recall.