An Efficient Learning-Based Solver for Two-Stage DC Optimal Power Flow with Feasibility Guarantees

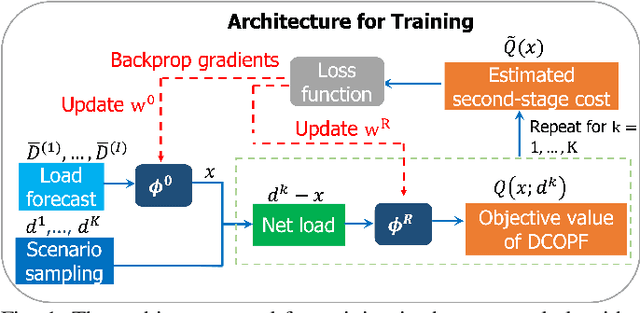
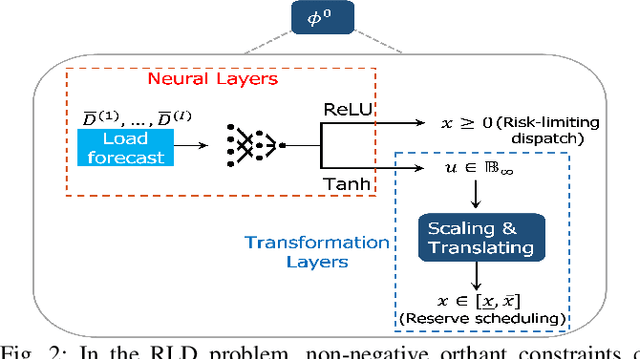
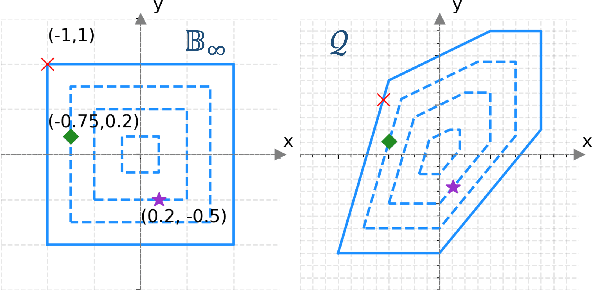
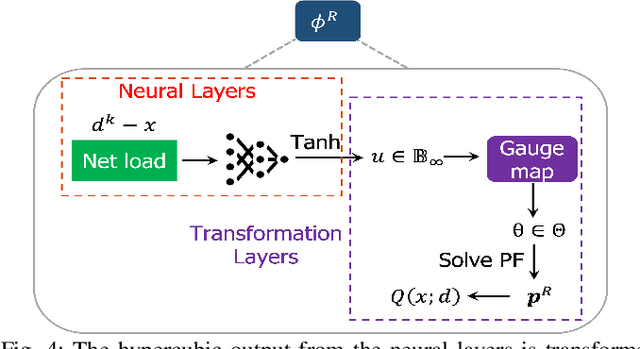
In this paper, we consider the scenario-based two-stage stochastic DC optimal power flow (OPF) problem for optimal and reliable dispatch when the load is facing uncertainty. Although this problem is a linear program, it remains computationally challenging to solve due to the large number of scenarios needed to accurately represent the uncertainties. To mitigate the computational issues, many techniques have been proposed to approximate the second-stage decisions so they can dealt more efficiently. The challenge of finding good policies to approximate the second-stage decisions is that these solutions need to be feasible, which has been difficult to achieve with existing policies. To address these challenges, this paper proposes a learning method to solve the two-stage problem in a more efficient and optimal way. A technique called the gauge map is incorporated into the learning architecture design to guarantee the learned solutions' feasibility to the network constraints. Namely, we can design policies that are feed forward functions that only output feasible solutions. Simulation results on standard IEEE systems show that, compared to iterative solvers and the widely used affine policy, our proposed method not only learns solutions of good quality but also accelerates the computation by orders of magnitude.

Interpreting Primal-Dual Algorithms for Constrained MARL

Constrained multiagent reinforcement learning (C-MARL) is gaining importance as MARL algorithms find new applications in real-world systems ranging from energy systems to drone swarms. Most C-MARL algorithms use a primal-dual approach to enforce constraints through a penalty function added to the reward. In this paper, we study the structural effects of this penalty term on the MARL problem. First, we show that the standard practice of using the constraint function as the penalty leads to a weak notion of safety. However, by making simple modifications to the penalty term, we can enforce meaningful probabilistic (chance and conditional value at risk) constraints. Second, we quantify the effect of the penalty term on the value function, uncovering an improved value estimation procedure. We use these insights to propose a constrained multiagent advantage actor critic (C-MAA2C) algorithm. Simulations in a simple constrained multiagent environment affirm that our reinterpretation of the primal-dual method in terms of probabilistic constraints is effective, and that our proposed value estimate accelerates convergence to a safe joint policy.