Lyapunov-Regularized Reinforcement Learning for Power System Transient Stability
Paper and Code
Mar 05, 2021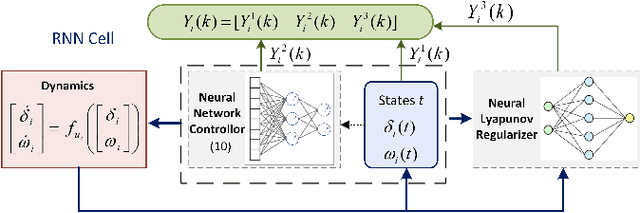

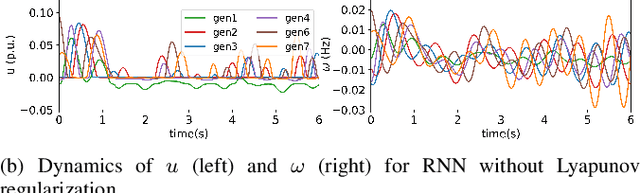
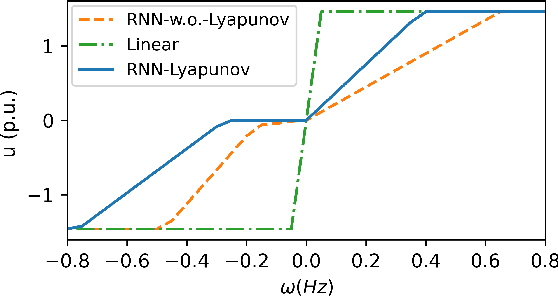
Transient stability of power systems is becoming increasingly important because of the growing integration of renewable resources. These resources lead to a reduction in mechanical inertia but also provide increased flexibility in frequency responses. Namely, their power electronic interfaces can implement almost arbitrary control laws. To design these controllers, reinforcement learning (RL) has emerged as a powerful method in searching for optimal non-linear control policy parameterized by neural networks. A key challenge is to enforce that a learned controller must be stabilizing. This paper proposes a Lyapunov regularized RL approach for optimal frequency control for transient stability in lossy networks. Because the lack of an analytical Lyapunov function, we learn a Lyapunov function parameterized by a neural network. The losses are specially designed with respect to the physical power system. The learned neural Lyapunov function is then utilized as a regularization to train the neural network controller by penalizing actions that violate the Lyapunov conditions. Case study shows that introducing the Lyapunov regularization enables the controller to be stabilizing and achieve smaller losses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge