Correctness Verification of Neural Networks Approximating Differential Equations

Verification of Neural Networks (NNs) that approximate the solution of Partial Differential Equations (PDEs) is a major milestone towards enhancing their trustworthiness and accelerating their deployment, especially for safety-critical systems. If successful, such NNs can become integral parts of simulation software tools which can accelerate the simulation of complex dynamic systems more than 100 times. However, the verification of these functions poses major challenges; it is not straightforward how to efficiently bound them or how to represent the derivative of the NN. This work addresses both these problems. First, we define the NN derivative as a finite difference approximation. Then, we formulate the PDE residual bounding problem alongside the Initial Value Problem's error propagation. Finally, for the first time, we tackle the problem of bounding an NN function without a priori knowledge of the output domain. For this, we build a parallel branching algorithm that combines the incomplete CROWN solver and Gradient Attack for termination and domain rejection conditions. We demonstrate the strengths and weaknesses of the proposed framework, and we suggest further work to enhance its efficiency.

Error estimation for physics-informed neural networks with implicit Runge-Kutta methods

The ability to accurately approximate trajectories of dynamical systems enables their analysis, prediction, and control. Neural network (NN)-based approximations have attracted significant interest due to fast evaluation with good accuracy over long integration time steps. In contrast to established numerical approximation schemes such as Runge-Kutta methods, the estimation of the error of the NN-based approximations proves to be difficult. In this work, we propose to use the NN's predictions in a high-order implicit Runge-Kutta (IRK) method. The residuals in the implicit system of equations can be related to the NN's prediction error, hence, we can provide an error estimate at several points along a trajectory. We find that this error estimate highly correlates with the NN's prediction error and that increasing the order of the IRK method improves this estimate. We demonstrate this estimation methodology for Physics-Informed Neural Network (PINNs) on the logistic equation as an illustrative example and then apply it to a four-state electric generator model that is regularly used in power system modelling.

Solving Differential-Algebraic Equations in Power Systems Dynamics with Neural Networks and Spatial Decomposition

The dynamics of the power system are described by a system of differential-algebraic equations. Time-domain simulations are used to understand the evolution of the system dynamics. These simulations can be computationally expensive due to the stiffness of the system which requires the use of finely discretized time-steps. By increasing the allowable time-step size, we aim to accelerate such simulations. In this paper, we use the observation that even though the individual components are described using both algebraic and differential equations, their coupling only involves algebraic equations. Following this observation, we use Neural Networks (NNs) to approximate the components' state evolution, leading to fast, accurate, and numerically stable approximators, which enable larger time-steps. To account for effects of the network on the components and vice-versa, the NNs take the temporal evolution of the coupling algebraic variables as an input for their prediction. We initially estimate this temporal evolution and then update it in an iterative fashion using the Newton-Raphson algorithm. The involved Jacobian matrix is calculated with Automatic Differentiation and its size depends only on the network size but not on the component dynamics. We demonstrate this NN-based simulator on the IEEE 9-bus test case with 3 generators.

Physics-Informed Neural Networks for Time-Domain Simulations: Accuracy, Computational Cost, and Flexibility

The simulation of power system dynamics poses a computationally expensive task. Considering the growing uncertainty of generation and demand patterns, thousands of scenarios need to be continuously assessed to ensure the safety of power systems. Physics-Informed Neural Networks (PINNs) have recently emerged as a promising solution for drastically accelerating computations of non-linear dynamical systems. This work investigates the applicability of these methods for power system dynamics, focusing on the dynamic response to load disturbances. Comparing the prediction of PINNs to the solution of conventional solvers, we find that PINNs can be 10 to 1000 times faster than conventional solvers. At the same time, we find them to be sufficiently accurate and numerically stable even for large time steps. To facilitate a deeper understanding, this paper also presents a new regularisation of Neural Network (NN) training by introducing a gradient-based term in the loss function. The resulting NNs, which we call dtNNs, help us deliver a comprehensive analysis about the strengths and weaknesses of the NN based approaches, how incorporating knowledge of the underlying physics affects NN performance, and how this compares with conventional solvers for power system dynamics.

Closing the Loop: A Framework for Trustworthy Machine Learning in Power Systems

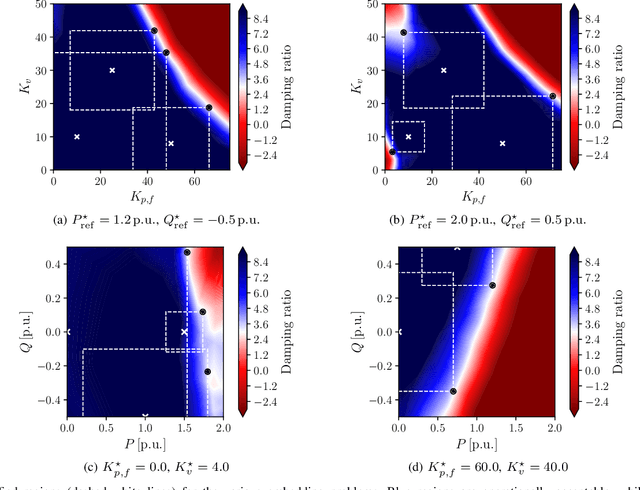
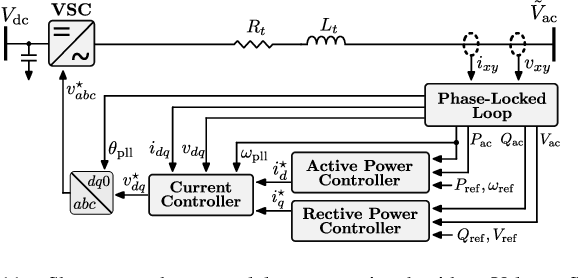
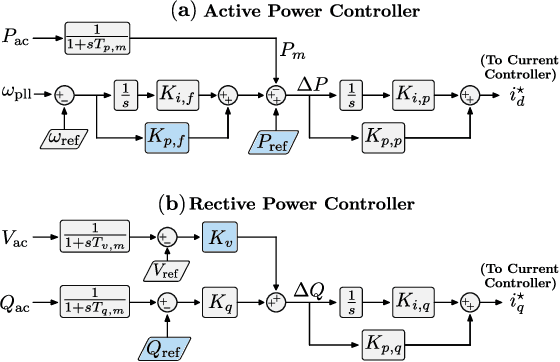
Deep decarbonization of the energy sector will require massive penetration of stochastic renewable energy resources and an enormous amount of grid asset coordination; this represents a challenging paradigm for the power system operators who are tasked with maintaining grid stability and security in the face of such changes. With its ability to learn from complex datasets and provide predictive solutions on fast timescales, machine learning (ML) is well-posed to help overcome these challenges as power systems transform in the coming decades. In this work, we outline five key challenges (dataset generation, data pre-processing, model training, model assessment, and model embedding) associated with building trustworthy ML models which learn from physics-based simulation data. We then demonstrate how linking together individual modules, each of which overcomes a respective challenge, at sequential stages in the machine learning pipeline can help enhance the overall performance of the training process. In particular, we implement methods that connect different elements of the learning pipeline through feedback, thus "closing the loop" between model training, performance assessments, and re-training. We demonstrate the effectiveness of this framework, its constituent modules, and its feedback connections by learning the N-1 small-signal stability margin associated with a detailed model of a proposed North Sea Wind Power Hub system.

Transient Stability Analysis with Physics-Informed Neural Networks

Solving the ordinary differential equations that govern the power system is an indispensable part in transient stability analysis. However, the traditionally applied methods either carry a significant computational burden, require model simplifications, or use overly conservative surrogate models. Neural networks can circumvent these limitations but are faced with high demands on the used datasets. Furthermore, they are agnostic to the underlying governing equations. Physics-informed neural network tackle this problem and we explore their advantages and challenges in this paper. We illustrate the findings on the Kundur two-area system and highlight possible pathways forward in developing this method further.

Contracting Neural-Newton Solver

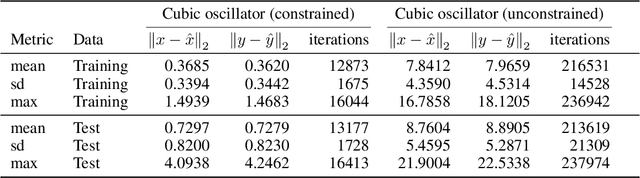
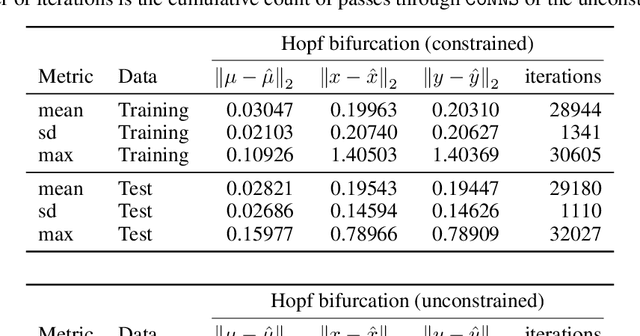
Recent advances in deep learning have set the focus on neural networks (NNs) that can successfully replace traditional numerical solvers in many applications, achieving impressive computing gains. One such application is time domain simulation, which is indispensable for the design, analysis and operation of many engineering systems. Simulating dynamical systems with implicit Newton-based solvers is a computationally heavy task, as it requires the solution of a parameterized system of differential and algebraic equations at each time step. A variety of NN-based methodologies have been shown to successfully approximate the dynamical trajectories computed by numerical time domain solvers at a fraction of the time. However, so far no previous NN-based model has explicitly captured the fact that any predicted point on the time domain trajectory also represents the fixed point of the numerical solver itself. As we show, explicitly capturing this property can lead to significantly increased NN accuracy and much smaller NN sizes. In this paper, we model the Newton solver at the heart of an implicit Runge-Kutta integrator as a contracting map iteratively seeking this fixed point. Our primary contribution is to develop a recurrent NN simulation tool, termed the Contracting Neural-Newton Solver (CoNNS), which explicitly captures the contracting nature of these Newton iterations. To build CoNNS, we train a feedforward NN and mimic this contraction behavior by embedding a series of training constraints which guarantee the mapping provided by the NN satisfies the Banach fixed-point theorem; thus, we are able to prove that successive passes through the NN are guaranteed to converge to a unique, fixed point.

Physics-Informed Neural Networks for Non-linear System Identification applied to Power System Dynamics

Varying power-infeed from converter-based generation units introduces great uncertainty on system parameters such as inertia and damping. As a consequence, system operators face increasing challenges in performing dynamic security assessment and taking real-time control actions. Exploiting the widespread deployment of phasor measurement units (PMUs) and aiming at developing a fast dynamic state and parameter estimation tool, this paper investigates the performance of Physics-Informed Neural Networks (PINN) for discovering the frequency dynamics of future power systems and monitoring the system inertia in real-time. PINNs have the potential to address challenges such as the stronger non-linearities of low-inertia systems, increased measurement noise, and limited availability of data. The estimator is demonstrated in several test cases using a 4-bus system, and compared with state of the art algorithms, such as the Unscented Kalman Filter (UKF), to assess its performance.