Contracting Neural-Newton Solver
Paper and Code
Jun 04, 2021
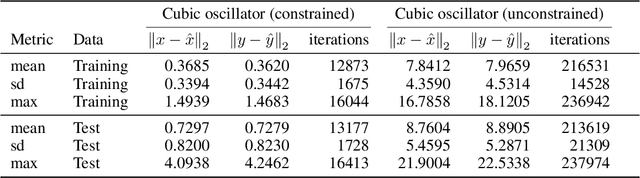

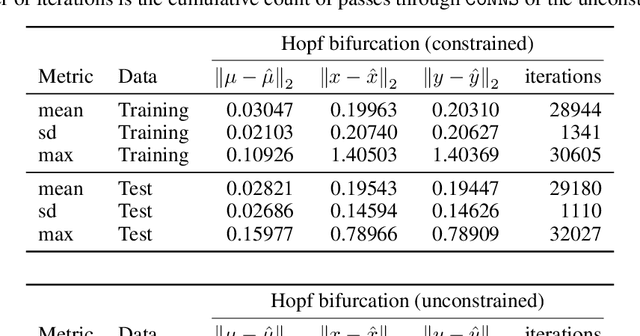
Recent advances in deep learning have set the focus on neural networks (NNs) that can successfully replace traditional numerical solvers in many applications, achieving impressive computing gains. One such application is time domain simulation, which is indispensable for the design, analysis and operation of many engineering systems. Simulating dynamical systems with implicit Newton-based solvers is a computationally heavy task, as it requires the solution of a parameterized system of differential and algebraic equations at each time step. A variety of NN-based methodologies have been shown to successfully approximate the dynamical trajectories computed by numerical time domain solvers at a fraction of the time. However, so far no previous NN-based model has explicitly captured the fact that any predicted point on the time domain trajectory also represents the fixed point of the numerical solver itself. As we show, explicitly capturing this property can lead to significantly increased NN accuracy and much smaller NN sizes. In this paper, we model the Newton solver at the heart of an implicit Runge-Kutta integrator as a contracting map iteratively seeking this fixed point. Our primary contribution is to develop a recurrent NN simulation tool, termed the Contracting Neural-Newton Solver (CoNNS), which explicitly captures the contracting nature of these Newton iterations. To build CoNNS, we train a feedforward NN and mimic this contraction behavior by embedding a series of training constraints which guarantee the mapping provided by the NN satisfies the Banach fixed-point theorem; thus, we are able to prove that successive passes through the NN are guaranteed to converge to a unique, fixed point.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge