Achieving the Tightest Relaxation of Sigmoids for Formal Verification

In the field of formal verification, Neural Networks (NNs) are typically reformulated into equivalent mathematical programs which are optimized over. To overcome the inherent non-convexity of these reformulations, convex relaxations of nonlinear activation functions are typically utilized. Common relaxations (i.e., static linear cuts) of "S-shaped" activation functions, however, can be overly loose, slowing down the overall verification process. In this paper, we derive tuneable hyperplanes which upper and lower bound the sigmoid activation function. When tuned in the dual space, these affine bounds smoothly rotate around the nonlinear manifold of the sigmoid activation function. This approach, termed $\alpha$-sig, allows us to tractably incorporate the tightest possible, element-wise convex relaxation of the sigmoid activation function into a formal verification framework. We embed these relaxations inside of large verification tasks and compare their performance to LiRPA and $\alpha$-CROWN, a state-of-the-art verification duo.

Global Performance Guarantees for Neural Network Models of AC Power Flow

Machine learning can generate black-box surrogate models which are both extremely fast and highly accurate. Rigorously verifying the accuracy of these black-box models, however, is computationally challenging. When it comes to power systems, learning AC power flow is the cornerstone of any machine learning surrogate model wishing to drastically accelerate computations, whether it is for optimization, control, or dynamics. This paper develops for the first time, to our knowledge, a tractable neural network verification procedure which incorporates the ground truth of the \emph{non-linear} AC power flow equations to determine worst-case neural network performance. Our approach, termed Sequential Targeted Tightening (STT), leverages a loosely convexified reformulation of the original verification problem, which is a mixed integer quadratic program (MIQP). Using the sequential addition of targeted cuts, we iteratively tighten our formulation until either the solution is sufficiently tight or a satisfactory performance guarantee has been generated. After learning neural network models of the 14, 57, 118, and 200-bus PGLib test cases, we compare the performance guarantees generated by our STT procedure with ones generated by a state-of-the-art MIQP solver, Gurobi 9.5. We show that STT often generates performance guarantees which are orders of magnitude tighter than the MIQP upper bound.

Emission-Aware Optimization of Gas Networks: Input-Convex Neural Network Approach

Gas network planning optimization under emission constraints prioritizes gas supply with the least CO$_2$ intensity. As this problem includes complex physical laws of gas flow, standard optimization solvers cannot guarantee convergence to a feasible solution. To address this issue, we develop an input-convex neural network (ICNN) aided optimization routine which incorporates a set of trained ICNNs approximating the gas flow equations with high precision. Numerical tests on the Belgium gas network demonstrate that the ICNN-aided optimization dominates non-convex and relaxation-based solvers, with larger optimality gains pertaining to stricter emission targets. Moreover, whenever the non-convex solver fails, the ICNN-aided optimization provides a feasible solution to network planning.

Closing the Loop: A Framework for Trustworthy Machine Learning in Power Systems

Deep decarbonization of the energy sector will require massive penetration of stochastic renewable energy resources and an enormous amount of grid asset coordination; this represents a challenging paradigm for the power system operators who are tasked with maintaining grid stability and security in the face of such changes. With its ability to learn from complex datasets and provide predictive solutions on fast timescales, machine learning (ML) is well-posed to help overcome these challenges as power systems transform in the coming decades. In this work, we outline five key challenges (dataset generation, data pre-processing, model training, model assessment, and model embedding) associated with building trustworthy ML models which learn from physics-based simulation data. We then demonstrate how linking together individual modules, each of which overcomes a respective challenge, at sequential stages in the machine learning pipeline can help enhance the overall performance of the training process. In particular, we implement methods that connect different elements of the learning pipeline through feedback, thus "closing the loop" between model training, performance assessments, and re-training. We demonstrate the effectiveness of this framework, its constituent modules, and its feedback connections by learning the N-1 small-signal stability margin associated with a detailed model of a proposed North Sea Wind Power Hub system.

Modeling the AC Power Flow Equations with Optimally Compact Neural Networks: Application to Unit Commitment

Nonlinear power flow constraints render a variety of power system optimization problems computationally intractable. Emerging research shows, however, that the nonlinear AC power flow equations can be successfully modeled using Neural Networks (NNs). These NNs can be exactly transformed into Mixed Integer Linear Programs (MILPs) and embedded inside challenging optimization problems, thus replacing nonlinearities that are intractable for many applications with tractable piecewise linear approximations. Such approaches, though, suffer from an explosion of the number of binary variables needed to represent the NN. Accordingly, this paper develops a technique for training an "optimally compact" NN, i.e., one that can represent the power flow equations with a sufficiently high degree of accuracy while still maintaining a tractable number of binary variables. We show that the resulting NN model is more expressive than both the DC and linearized power flow approximations when embedded inside of a challenging optimization problem (i.e., the AC unit commitment problem).

Contracting Neural-Newton Solver

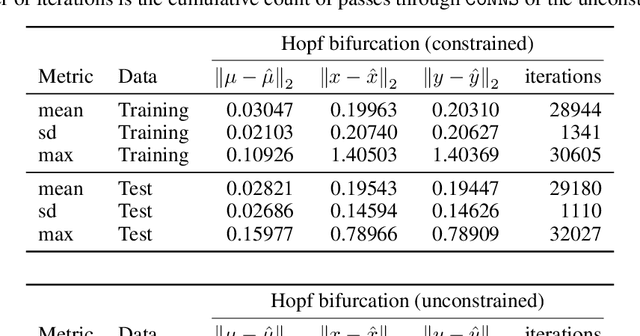
Recent advances in deep learning have set the focus on neural networks (NNs) that can successfully replace traditional numerical solvers in many applications, achieving impressive computing gains. One such application is time domain simulation, which is indispensable for the design, analysis and operation of many engineering systems. Simulating dynamical systems with implicit Newton-based solvers is a computationally heavy task, as it requires the solution of a parameterized system of differential and algebraic equations at each time step. A variety of NN-based methodologies have been shown to successfully approximate the dynamical trajectories computed by numerical time domain solvers at a fraction of the time. However, so far no previous NN-based model has explicitly captured the fact that any predicted point on the time domain trajectory also represents the fixed point of the numerical solver itself. As we show, explicitly capturing this property can lead to significantly increased NN accuracy and much smaller NN sizes. In this paper, we model the Newton solver at the heart of an implicit Runge-Kutta integrator as a contracting map iteratively seeking this fixed point. Our primary contribution is to develop a recurrent NN simulation tool, termed the Contracting Neural-Newton Solver (CoNNS), which explicitly captures the contracting nature of these Newton iterations. To build CoNNS, we train a feedforward NN and mimic this contraction behavior by embedding a series of training constraints which guarantee the mapping provided by the NN satisfies the Banach fixed-point theorem; thus, we are able to prove that successive passes through the NN are guaranteed to converge to a unique, fixed point.