Scalable Exact Verification of Optimization Proxies for Large-Scale Optimal Power Flow

Optimal Power Flow (OPF) is a valuable tool for power system operators, but it is a difficult problem to solve for large systems. Machine Learning (ML) algorithms, especially Neural Networks-based (NN) optimization proxies, have emerged as a promising new tool for solving OPF, by estimating the OPF solution much faster than traditional methods. However, these ML algorithms act as black boxes, and it is hard to assess their worst-case performance across the entire range of possible inputs than an OPF can have. Previous work has proposed a mixed-integer programming-based methodology to quantify the worst-case violations caused by a NN trained to estimate the OPF solution, throughout the entire input domain. This approach, however, does not scale well to large power systems and more complex NN models. This paper addresses these issues by proposing a scalable algorithm to compute worst-case violations of NN proxies used for approximating large power systems within a reasonable time limit. This will help build trust in ML models to be deployed in large industry-scale power grids.

Enriching Neural Network Training Dataset to Improve Worst-Case Performance Guarantees

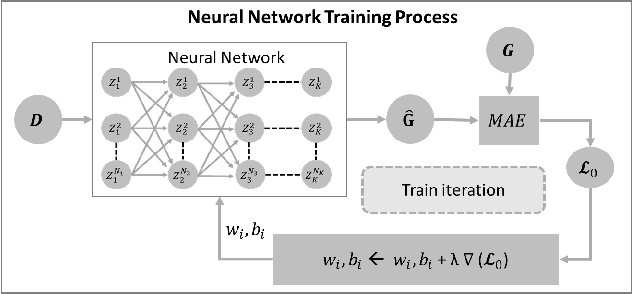
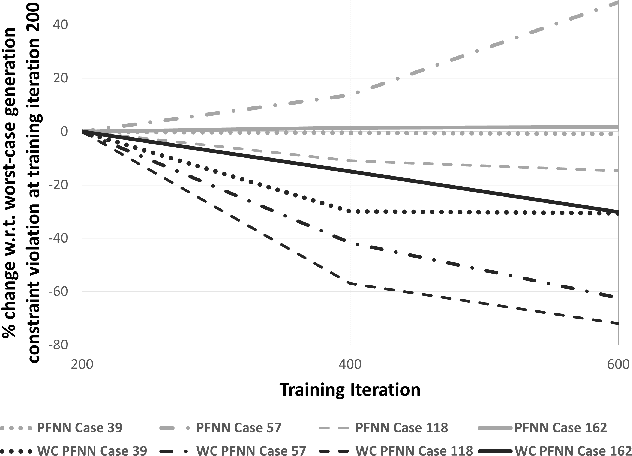
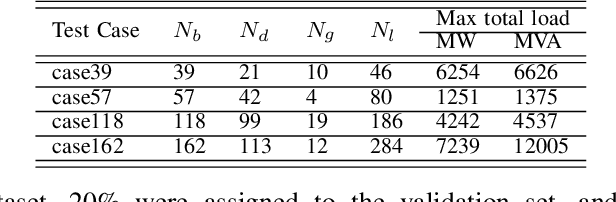
Machine learning algorithms, especially Neural Networks (NNs), are a valuable tool used to approximate non-linear relationships, like the AC-Optimal Power Flow (AC-OPF), with considerable accuracy -- and achieving a speedup of several orders of magnitude when deployed for use. Often in power systems literature, the NNs are trained with a fixed dataset generated prior to the training process. In this paper, we show that adapting the NN training dataset during training can improve the NN performance and substantially reduce its worst-case violations. This paper proposes an algorithm that identifies and enriches the training dataset with critical datapoints that reduce the worst-case violations and deliver a neural network with improved worst-case performance guarantees. We demonstrate the performance of our algorithm in four test power systems, ranging from 39-buses to 162-buses.

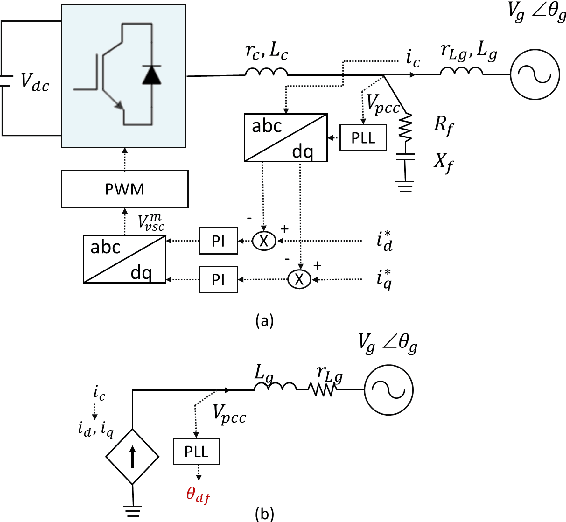
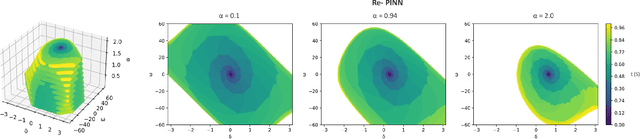
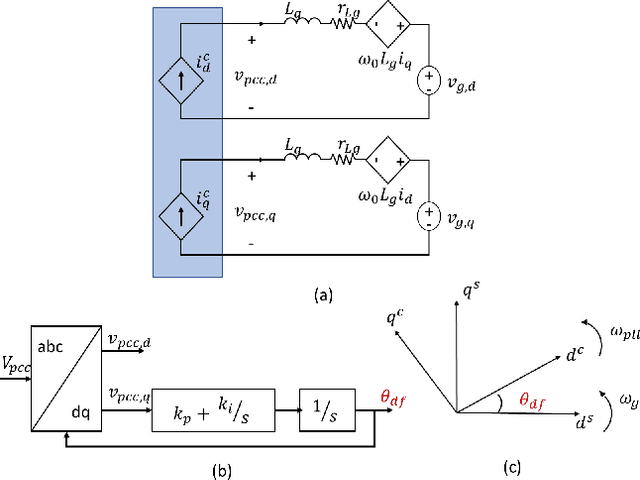
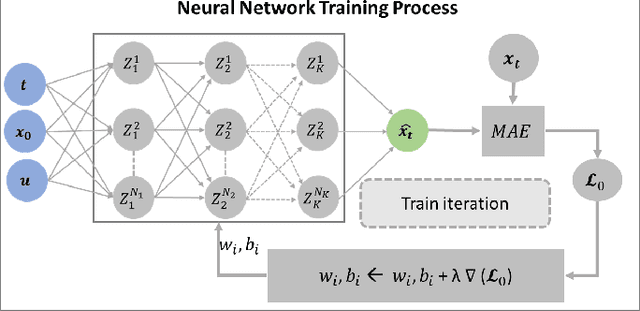
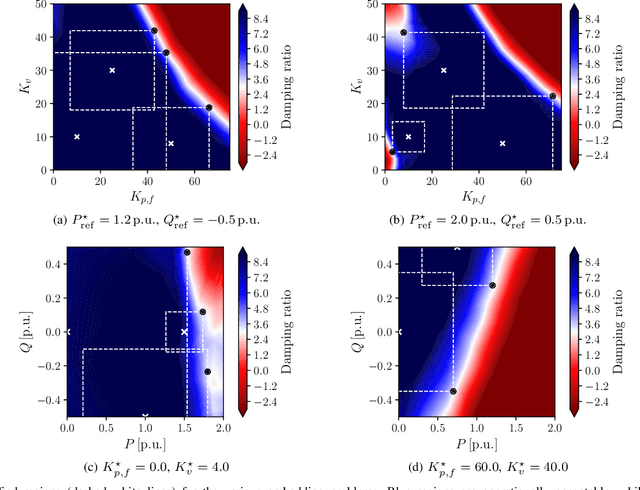
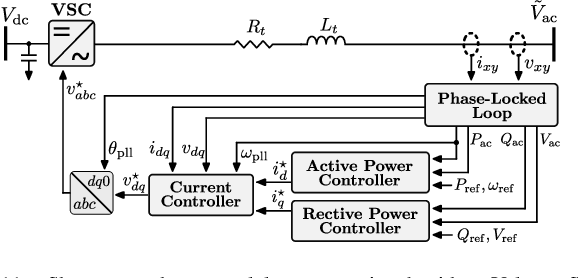
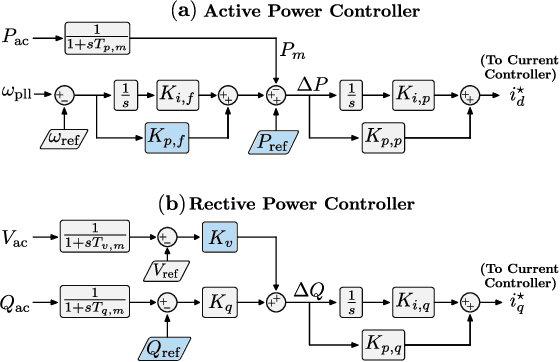
Physics Informed Neural Networks for Phase Locked Loop Transient Stability Assessment

A significant increase in renewable energy production is necessary to achieve the UN's net-zero emission targets for 2050. Using power-electronic controllers, such as Phase Locked Loops (PLLs), to keep grid-tied renewable resources in synchronism with the grid can cause fast transient behavior during grid faults leading to instability. However, assessing all the probable scenarios is impractical, so determining the stability boundary or region of attraction (ROA) is necessary. However, using EMT simulations or Reduced-order models (ROMs) to accurately determine the ROA is computationally expensive. Alternatively, Machine Learning (ML) models have been proposed as an efficient method to predict stability. However, traditional ML algorithms require large amounts of labeled data for training, which is computationally expensive. This paper proposes a Physics-Informed Neural Network (PINN) architecture that accurately predicts the nonlinear transient dynamics of a PLL controller under fault with less labeled training data. The proposed PINN algorithm can be incorporated into conventional simulations, accelerating EMT simulations or ROMs by over 100 times. The PINN algorithm's performance is compared against a ROM and an EMT simulation in PSCAD for the CIGRE benchmark model C4.49, demonstrating its ability to accurately approximate trajectories and ROAs of a PLL controller under varying grid impedance.

Minimizing Worst-Case Violations of Neural Networks

Machine learning (ML) algorithms are remarkably good at approximating complex non-linear relationships. Most ML training processes, however, are designed to deliver ML tools with good average performance, but do not offer any guarantees about their worst-case estimation error. For safety-critical systems such as power systems, this places a major barrier for their adoption. So far, approaches could determine the worst-case violations of only trained ML algorithms. To the best of our knowledge, this is the first paper to introduce a neural network training procedure designed to achieve both a good average performance and minimum worst-case violations. Using the Optimal Power Flow (OPF) problem as a guiding application, our approach (i) introduces a framework that reduces the worst-case generation constraint violations during training, incorporating them as a differentiable optimization layer; and (ii) presents a neural network sequential learning architecture to significantly accelerate it. We demonstrate the proposed architecture on four different test systems ranging from 39 buses to 162 buses, for both AC-OPF and DC-OPF applications.

Closing the Loop: A Framework for Trustworthy Machine Learning in Power Systems

Deep decarbonization of the energy sector will require massive penetration of stochastic renewable energy resources and an enormous amount of grid asset coordination; this represents a challenging paradigm for the power system operators who are tasked with maintaining grid stability and security in the face of such changes. With its ability to learn from complex datasets and provide predictive solutions on fast timescales, machine learning (ML) is well-posed to help overcome these challenges as power systems transform in the coming decades. In this work, we outline five key challenges (dataset generation, data pre-processing, model training, model assessment, and model embedding) associated with building trustworthy ML models which learn from physics-based simulation data. We then demonstrate how linking together individual modules, each of which overcomes a respective challenge, at sequential stages in the machine learning pipeline can help enhance the overall performance of the training process. In particular, we implement methods that connect different elements of the learning pipeline through feedback, thus "closing the loop" between model training, performance assessments, and re-training. We demonstrate the effectiveness of this framework, its constituent modules, and its feedback connections by learning the N-1 small-signal stability margin associated with a detailed model of a proposed North Sea Wind Power Hub system.

Physics-Informed Neural Networks for AC Optimal Power Flow

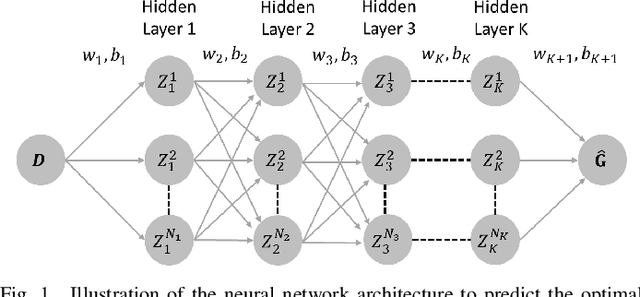
This paper introduces, for the first time to our knowledge, physics-informed neural networks to accurately estimate the AC-OPF result and delivers rigorous guarantees about their performance. Power system operators, along with several other actors, are increasingly using Optimal Power Flow (OPF) algorithms for a wide number of applications, including planning and real-time operations. However, in its original form, the AC Optimal Power Flow problem is often challenging to solve as it is non-linear and non-convex. Besides the large number of approximations and relaxations, recent efforts have also been focusing on Machine Learning approaches, especially neural networks. So far, however, these approaches have only partially considered the wide number of physical models available during training. And, more importantly, they have offered no guarantees about potential constraint violations of their output. Our approach (i) introduces the AC power flow equations inside neural network training and (ii) integrates methods that rigorously determine and reduce the worst-case constraint violations across the entire input domain, while maintaining the optimality of the prediction. We demonstrate how physics-informed neural networks achieve higher accuracy and lower constraint violations than standard neural networks, and show how we can further reduce the worst-case violations for all neural networks.

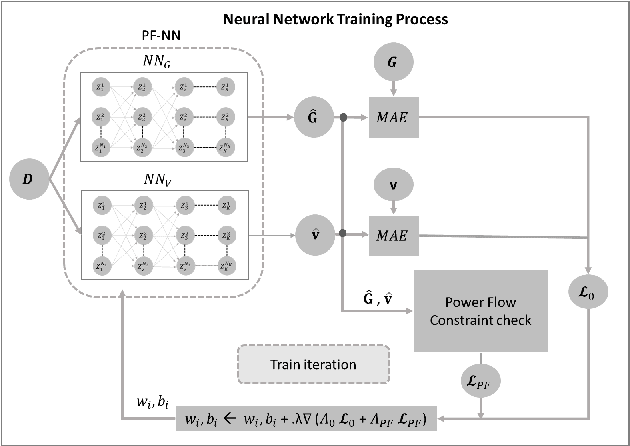
Physics-Informed Neural Networks for Minimising Worst-Case Violations in DC Optimal Power Flow

Physics-informed neural networks exploit the existing models of the underlying physical systems to generate higher accuracy results with fewer data. Such approaches can help drastically reduce the computation time and generate a good estimate of computationally intensive processes in power systems, such as dynamic security assessment or optimal power flow. Combined with the extraction of worst-case guarantees for the neural network performance, such neural networks can be applied in safety-critical applications in power systems and build a high level of trust among power system operators. This paper takes the first step and applies, for the first time to our knowledge, Physics-Informed Neural Networks with Worst-Case Guarantees for the DC Optimal Power Flow problem. We look for guarantees related to (i) maximum constraint violations, (ii) maximum distance between predicted and optimal decision variables, and (iii) maximum sub-optimality in the entire input domain. In a range of PGLib-OPF networks, we demonstrate how physics-informed neural networks can be supplied with worst-case guarantees and how they can lead to reduced worst-case violations compared with conventional neural networks.