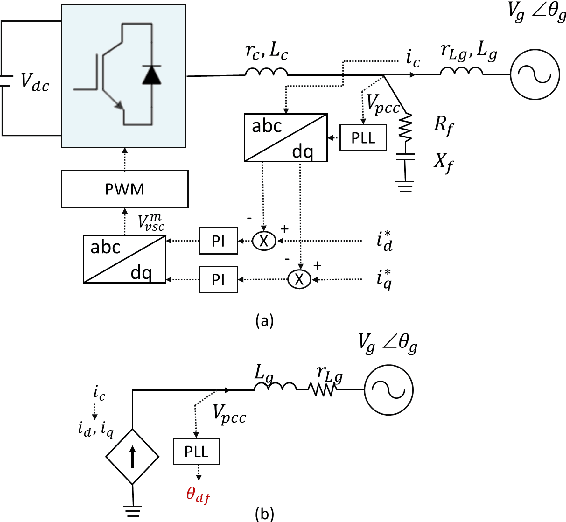
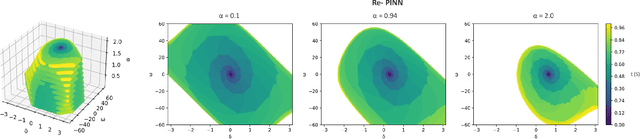
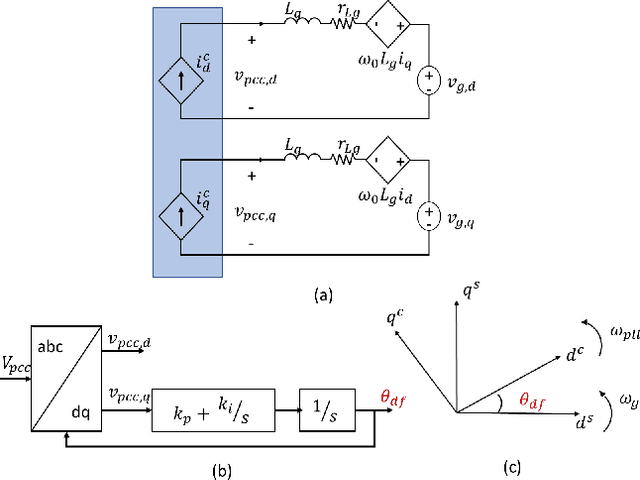
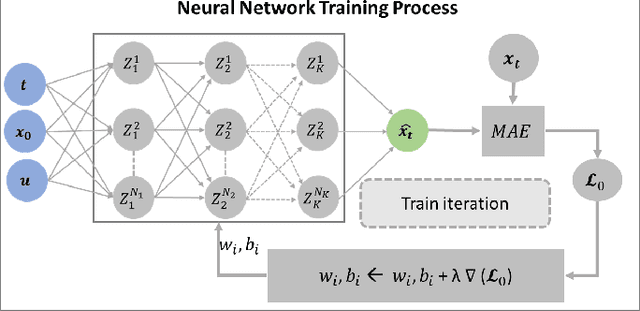
Physics Informed Neural Networks for Phase Locked Loop Transient Stability Assessment

A significant increase in renewable energy production is necessary to achieve the UN's net-zero emission targets for 2050. Using power-electronic controllers, such as Phase Locked Loops (PLLs), to keep grid-tied renewable resources in synchronism with the grid can cause fast transient behavior during grid faults leading to instability. However, assessing all the probable scenarios is impractical, so determining the stability boundary or region of attraction (ROA) is necessary. However, using EMT simulations or Reduced-order models (ROMs) to accurately determine the ROA is computationally expensive. Alternatively, Machine Learning (ML) models have been proposed as an efficient method to predict stability. However, traditional ML algorithms require large amounts of labeled data for training, which is computationally expensive. This paper proposes a Physics-Informed Neural Network (PINN) architecture that accurately predicts the nonlinear transient dynamics of a PLL controller under fault with less labeled training data. The proposed PINN algorithm can be incorporated into conventional simulations, accelerating EMT simulations or ROMs by over 100 times. The PINN algorithm's performance is compared against a ROM and an EMT simulation in PSCAD for the CIGRE benchmark model C4.49, demonstrating its ability to accurately approximate trajectories and ROAs of a PLL controller under varying grid impedance.

Learning Optimal Power Flow: Worst-Case Guarantees for Neural Networks

This paper introduces for the first time a framework to obtain provable worst-case guarantees for neural network performance, using learning for optimal power flow (OPF) problems as a guiding example. Neural networks have the potential to substantially reduce the computing time of OPF solutions. However, the lack of guarantees for their worst-case performance remains a major barrier for their adoption in practice. This work aims to remove this barrier. We formulate mixed-integer linear programs to obtain worst-case guarantees for neural network predictions related to (i) maximum constraint violations, (ii) maximum distances between predicted and optimal decision variables, and (iii) maximum sub-optimality. We demonstrate our methods on a range of PGLib-OPF networks up to 300 buses. We show that the worst-case guarantees can be up to one order of magnitude larger than the empirical lower bounds calculated with conventional methods. More importantly, we show that the worst-case predictions appear at the boundaries of the training input domain, and we demonstrate how we can systematically reduce the worst-case guarantees by training on a larger input domain than the domain they are evaluated on.

Neural Networks for Encoding Dynamic Security-Constrained Optimal Power Flow to Mixed-Integer Linear Programs

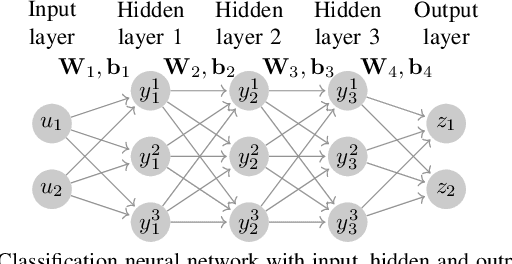
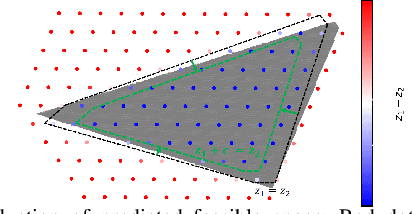
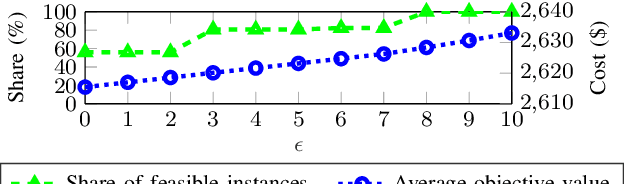
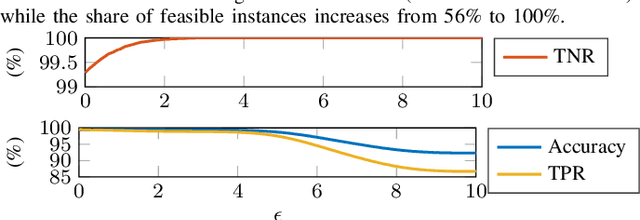
This paper introduces a framework to capture previously intractable optimization constraints and transform them to a mixed-integer linear program, through the use of neural networks. We encode the feasible space of optimization problems characterized by both tractable and intractable constraints, e.g. differential equations, to a neural network. Leveraging an exact mixed-integer reformulation of neural networks, we solve mixed-integer linear programs that accurately approximate solutions to the originally intractable non-linear optimization problem. We apply our methods to the AC optimal power flow problem (AC-OPF), where directly including dynamic security constraints renders the AC-OPF intractable. Our proposed approach has the potential to be significantly more scalable than traditional approaches. We demonstrate our approach for power system operation considering N-1 security and small-signal stability, showing how it can efficiently obtain cost-optimal solutions which at the same time satisfy both static and dynamic security constraints.

Physics-Informed Neural Networks for Power Systems

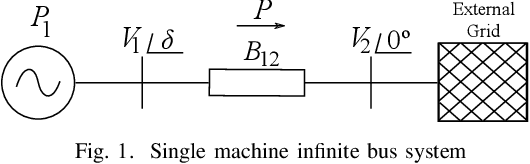
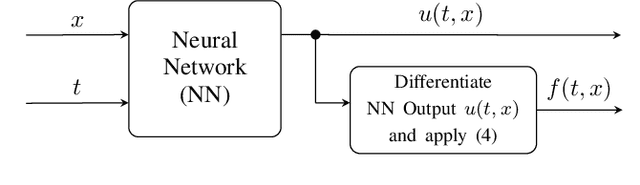
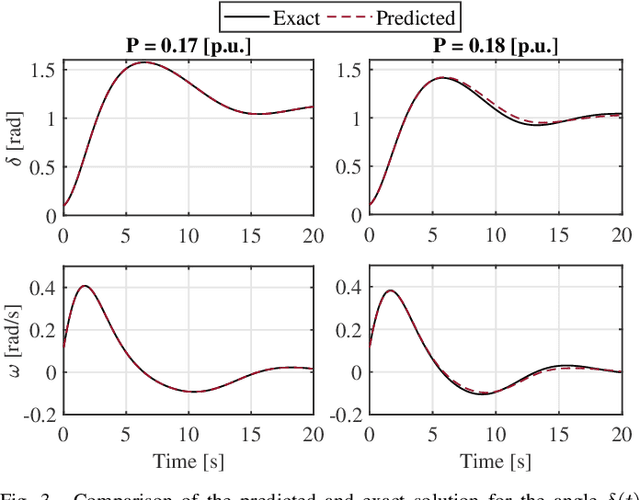
This paper introduces for the first time, to our knowledge, a framework for physics-informed neural networks in power system applications. Exploiting the underlying physical laws governing power systems, and inspired by recent developments in the field of machine learning, this paper proposes a neural network training procedure that can make use of the wide range of mathematical models describing power system behavior, both in steady-state and in dynamics. Physics-informed neural networks require substantially less training data and result in much simpler neural network structures, while achieving high accuracy. This work unlocks a range of opportunities in power systems, being able to determine dynamic states, such as rotor angles and frequency, and uncertain parameters such as inertia and damping at a fraction of the computational time required by conventional methods. This paper focuses on introducing the framework and showcases its potential using a single-machine infinite bus system as a guiding example. Physics-informed neural networks are shown to accurately determine rotor angle and frequency up to 87 times faster than conventional methods.

Verification of Neural Network Behaviour: Formal Guarantees for Power System Applications

This paper presents for the first time, to our knowledge, a framework for verifying neural network behavior in power systems applications. Up to this moment, neural networks have been applied in power systems as a black-box; this has presented a major barrier for their adoption in practice. Developing a rigorous framework based on mixed integer linear programming, our methods can determine the range of inputs that neural networks classify as safe or unsafe, and are able to identify adversarial examples. Such methods have the potential to build the missing trust of power system operators on neural networks, and unlock a series of new applications in power systems. This paper presents the main theoretical framework and addresses concerns related to scalability and accuracy. We demonstrate our methods on the IEEE 9-bus, 14-bus, and 162-bus systems, treating both N-1 security and small-signal stability.