Data driven approach towards more efficient Newton-Raphson power flow calculation for distribution grids

Power flow (PF) calculations are fundamental to power system analysis to ensure stable and reliable grid operation. The Newton-Raphson (NR) method is commonly used for PF analysis due to its rapid convergence when initialized properly. However, as power grids operate closer to their capacity limits, ill-conditioned cases and convergence issues pose significant challenges. This work, therefore, addresses these challenges by proposing strategies to improve NR initialization, hence minimizing iterations and avoiding divergence. We explore three approaches: (i) an analytical method that estimates the basin of attraction using mathematical bounds on voltages, (ii) Two data-driven models leveraging supervised learning or physics-informed neural networks (PINNs) to predict optimal initial guesses, and (iii) a reinforcement learning (RL) approach that incrementally adjusts voltages to accelerate convergence. These methods are tested on benchmark systems. This research is particularly relevant for modern power systems, where high penetration of renewables and decentralized generation require robust and scalable PF solutions. In experiments, all three proposed methods demonstrate a strong ability to provide an initial guess for Newton-Raphson method to converge with fewer steps. The findings provide a pathway for more efficient real-time grid operations, which, in turn, support the transition toward smarter and more resilient electricity networks.

Adaptive Informed Deep Neural Networks for Power Flow Analysis

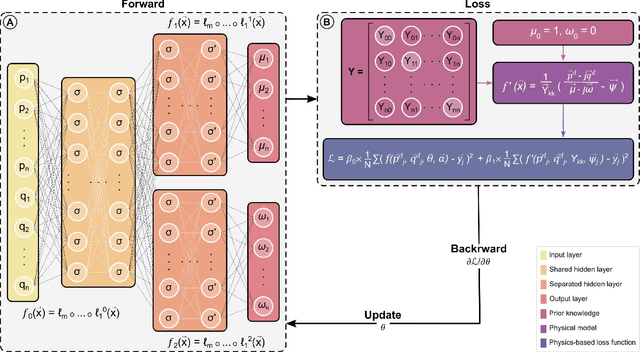
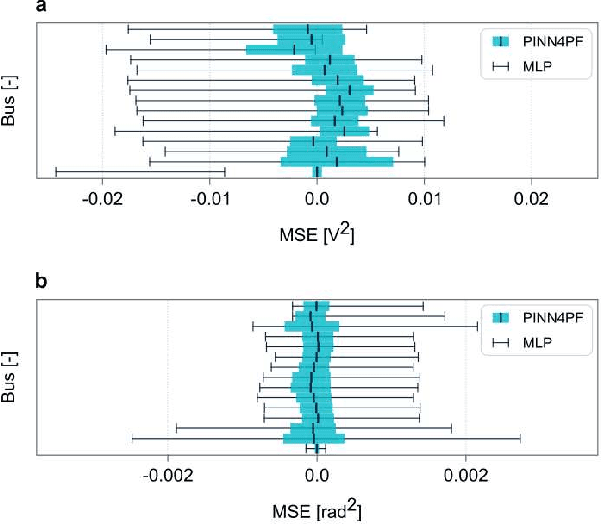
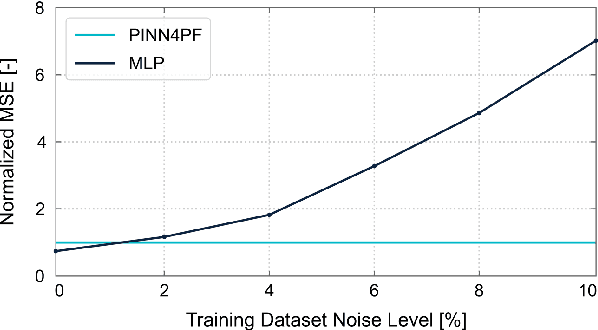
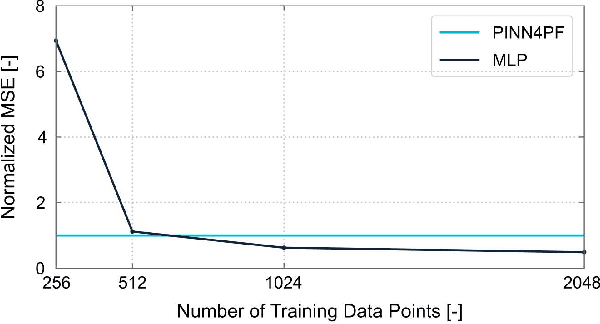
This study introduces PINN4PF, an end-to-end deep learning architecture for power flow (PF) analysis that effectively captures the nonlinear dynamics of large-scale modern power systems. The proposed neural network (NN) architecture consists of two important advancements in the training pipeline: (A) a double-head feed-forward NN that aligns with PF analysis, including an activation function that adjusts to active and reactive power consumption patterns, and (B) a physics-based loss function that partially incorporates power system topology information. The effectiveness of the proposed architecture is illustrated through 4-bus, 15-bus, 290-bus, and 2224-bus test systems and is evaluated against two baselines: a linear regression model (LR) and a black-box NN (MLP). The comparison is based on (i) generalization ability, (ii) robustness, (iii) impact of training dataset size on generalization ability, (iv) accuracy in approximating derived PF quantities (specifically line current, line active power, and line reactive power), and (v) scalability. Results demonstrate that PINN4PF outperforms both baselines across all test systems by up to two orders of magnitude not only in terms of direct criteria, e.g., generalization ability but also in terms of approximating derived physical quantities.

Quantum Neural Networks for Power Flow Analysis

This paper explores the potential application of quantum and hybrid quantum-classical neural networks in power flow analysis. Experiments are conducted using two small-size datasets based on the IEEE 4-bus and 33-bus test systems. A systematic performance comparison is also conducted among quantum, hybrid quantum-classical, and classical neural networks. The comparison is based on (i) generalization ability, (ii) robustness, (iii) training dataset size needed, (iv) training error. (v) training computational time, and (vi) training process stability. The results show that the developed quantum-classical neural network outperforms both quantum and classical neural networks, and hence can improve deep learning-based power flow analysis in the noisy-intermediate-scale quantum (NISQ) era.