Learning to Solve the AC Optimal Power Flow via a Lagrangian Approach
Paper and Code
Oct 04, 2021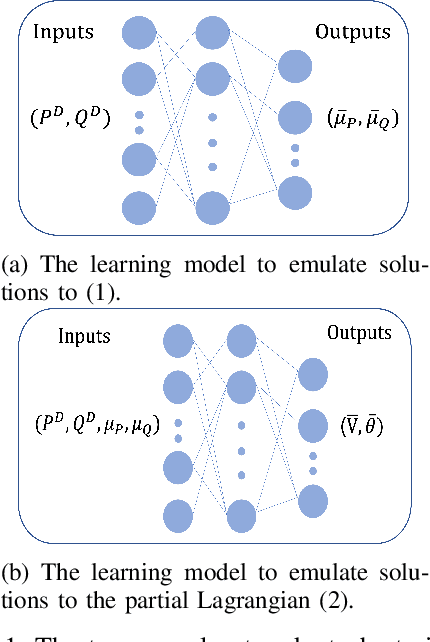
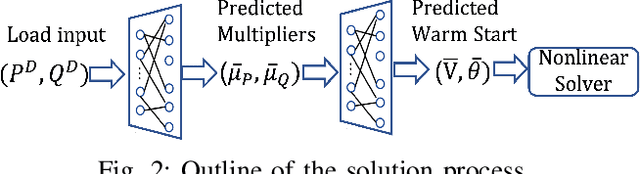
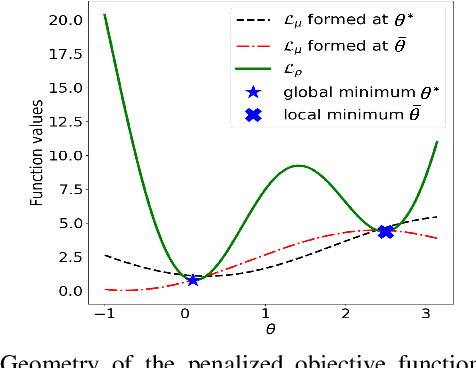
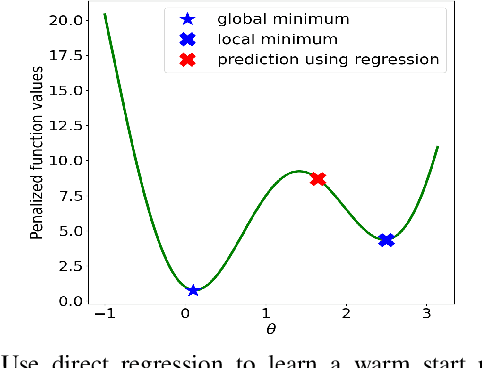
Using deep neural networks to predict the solutions of AC optimal power flow (ACOPF) problems has been an active direction of research. However, because the ACOPF is nonconvex, it is difficult to construct a good data set that contains mostly globally optimal solutions. To overcome the challenge that the training data may contain suboptimal solutions, we propose a Lagrangian-based approach. First, we use a neural network to learn the dual variables of the ACOPF problem. Then we use a second neural network to predict solutions of the partial Lagrangian from the predicted dual variables. Since the partial Lagrangian has a much better optimization landscape, we use the predicted solutions from the neural network as a warm start for the ACOPF problem. Using standard and modified IEEE 22-bus, 39-bus, and 118-bus networks, we show that our approach is able to obtain the globally optimal cost even when the training data is mostly comprised of suboptimal solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge