Offline Clustering of Preference Learning with Active-data Augmentation

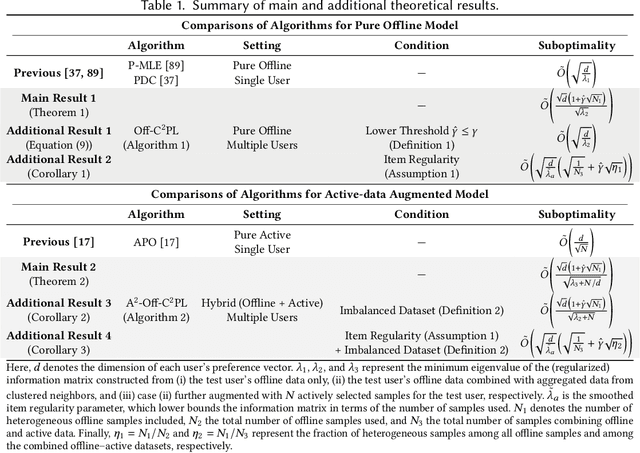
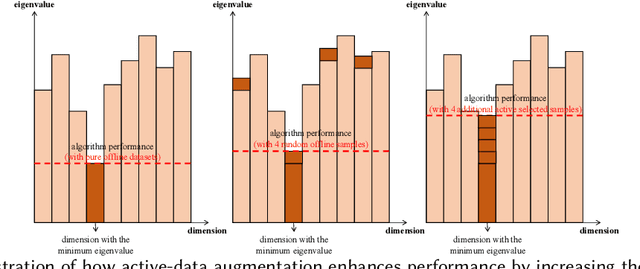
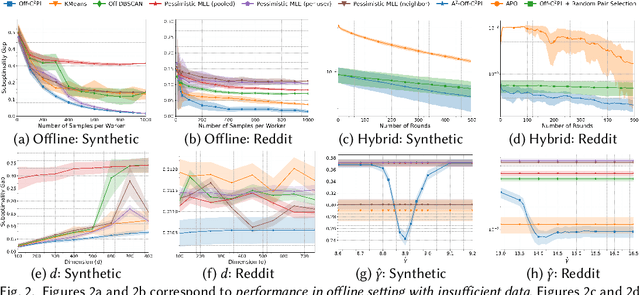
Preference learning from pairwise feedback is a widely adopted framework in applications such as reinforcement learning with human feedback and recommendations. In many practical settings, however, user interactions are limited or costly, making offline preference learning necessary. Moreover, real-world preference learning often involves users with different preferences. For example, annotators from different backgrounds may rank the same responses differently. This setting presents two central challenges: (1) identifying similarity across users to effectively aggregate data, especially under scenarios where offline data is imbalanced across dimensions, and (2) handling the imbalanced offline data where some preference dimensions are underrepresented. To address these challenges, we study the Offline Clustering of Preference Learning problem, where the learner has access to fixed datasets from multiple users with potentially different preferences and aims to maximize utility for a test user. To tackle the first challenge, we first propose Off-C$^2$PL for the pure offline setting, where the learner relies solely on offline data. Our theoretical analysis provides a suboptimality bound that explicitly captures the tradeoff between sample noise and bias. To address the second challenge of inbalanced data, we extend our framework to the setting with active-data augmentation where the learner is allowed to select a limited number of additional active-data for the test user based on the cluster structure learned by Off-C$^2$PL. In this setting, our second algorithm, A$^2$-Off-C$^2$PL, actively selects samples that target the least-informative dimensions of the test user's preference. We prove that these actively collected samples contribute more effectively than offline ones. Finally, we validate our theoretical results through simulations on synthetic and real-world datasets.

Heterogeneous Multi-agent Multi-armed Bandits on Stochastic Block Models

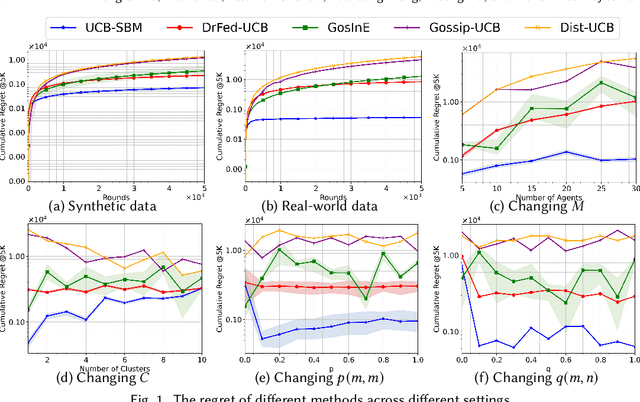
We study a novel heterogeneous multi-agent multi-armed bandit problem with a cluster structure induced by stochastic block models, influencing not only graph topology, but also reward heterogeneity. Specifically, agents are distributed on random graphs based on stochastic block models - a generalized Erdos-Renyi model with heterogeneous edge probabilities: agents are grouped into clusters (known or unknown); edge probabilities for agents within the same cluster differ from those across clusters. In addition, the cluster structure in stochastic block model also determines our heterogeneous rewards. Rewards distributions of the same arm vary across agents in different clusters but remain consistent within a cluster, unifying homogeneous and heterogeneous settings and varying degree of heterogeneity, and rewards are independent samples from these distributions. The objective is to minimize system-wide regret across all agents. To address this, we propose a novel algorithm applicable to both known and unknown cluster settings. The algorithm combines an averaging-based consensus approach with a newly introduced information aggregation and weighting technique, resulting in a UCB-type strategy. It accounts for graph randomness, leverages both intra-cluster (homogeneous) and inter-cluster (heterogeneous) information from rewards and graphs, and incorporates cluster detection for unknown cluster settings. We derive optimal instance-dependent regret upper bounds of order $\log{T}$ under sub-Gaussian rewards. Importantly, our regret bounds capture the degree of heterogeneity in the system (an additional layer of complexity), exhibit smaller constants, scale better for large systems, and impose significantly relaxed assumptions on edge probabilities. In contrast, prior works have not accounted for this refined problem complexity, rely on more stringent assumptions, and exhibit limited scalability.

Multi-Agent Stochastic Bandits Robust to Adversarial Corruptions

We study the problem of multi-agent multi-armed bandits with adversarial corruption in a heterogeneous setting, where each agent accesses a subset of arms. The adversary can corrupt the reward observations for all agents. Agents share these corrupted rewards with each other, and the objective is to maximize the cumulative total reward of all agents (and not be misled by the adversary). We propose a multi-agent cooperative learning algorithm that is robust to adversarial corruptions. For this newly devised algorithm, we demonstrate that an adversary with an unknown corruption budget $C$ only incurs an additive $O((L / L_{\min}) C)$ term to the standard regret of the model in non-corruption settings, where $L$ is the total number of agents, and $L_{\min}$ is the minimum number of agents with mutual access to an arm. As a side-product, our algorithm also improves the state-of-the-art regret bounds when reducing to both the single-agent and homogeneous multi-agent scenarios, tightening multiplicative $K$ (the number of arms) and $L$ (the number of agents) factors, respectively.