Your Absorbing Discrete Diffusion Secretly Models the Conditional Distributions of Clean Data

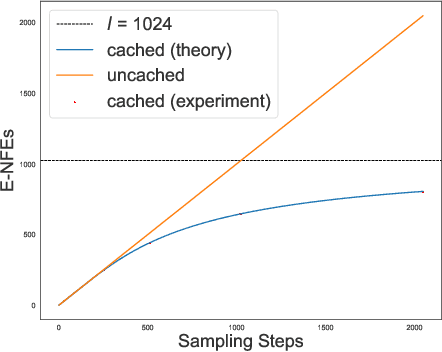
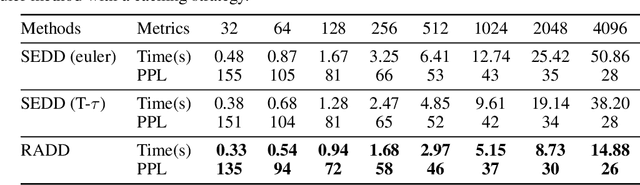
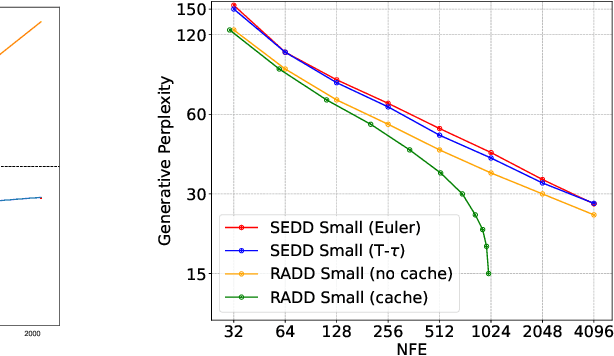
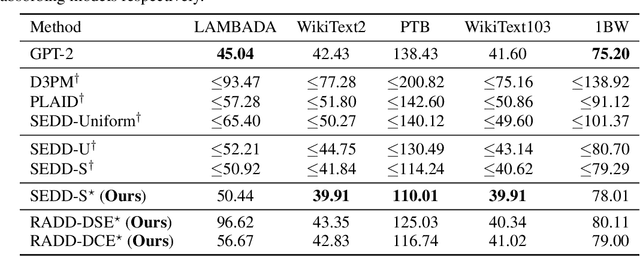
Discrete diffusion models with absorbing processes have shown promise in language modeling. The key quantities to be estimated are the ratios between the marginal probabilities of two transitive states at all timesteps, called the concrete score. In this paper, we reveal that the concrete score in absorbing diffusion can be expressed as conditional probabilities of clean data, multiplied by a time-dependent scalar in an analytic form. Motivated by the finding, we propose reparameterized absorbing discrete diffusion (RADD), a dedicated diffusion model that characterizes the time-independent conditional probabilities. Besides its simplicity, RADD can reduce the number of function evaluations (NFEs) by caching the output of the time-independent network when the noisy sample remains unchanged in a sampling interval. Empirically, RADD is up to 3.5 times faster while consistently achieving a better performance than the strongest baseline. Built upon the new factorization of the concrete score, we further prove a surprising result that the exact likelihood of absorbing diffusion can be rewritten to a simple form (named denoising cross-entropy) and then estimated efficiently by the Monte Carlo method. The resulting approach also applies to the original parameterization of the concrete score. It significantly advances the state-of-the-art discrete diffusion on 5 zero-shot language modeling benchmarks (measured by perplexity) at the GPT-2 scale.