LLaDA 1.5: Variance-Reduced Preference Optimization for Large Language Diffusion Models

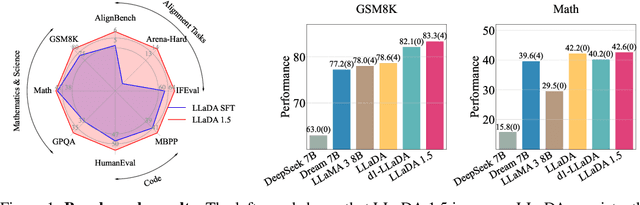
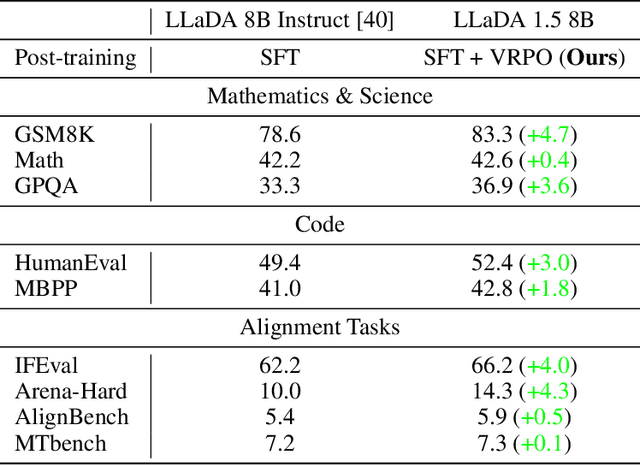
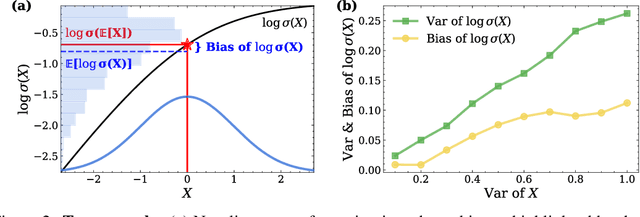
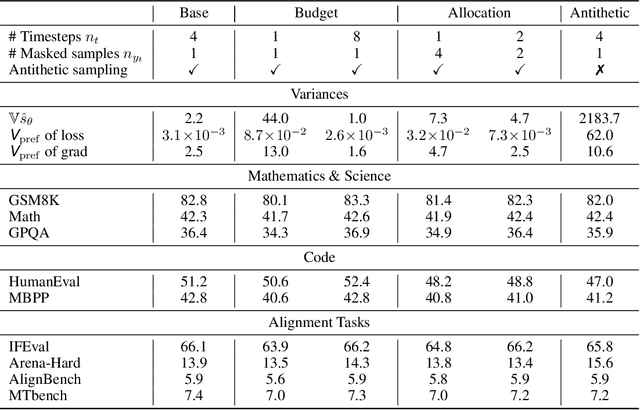
While Masked Diffusion Models (MDMs), such as LLaDA, present a promising paradigm for language modeling, there has been relatively little effort in aligning these models with human preferences via reinforcement learning. The challenge primarily arises from the high variance in Evidence Lower Bound (ELBO)-based likelihood estimates required for preference optimization. To address this issue, we propose Variance-Reduced Preference Optimization (VRPO), a framework that formally analyzes the variance of ELBO estimators and derives bounds on both the bias and variance of preference optimization gradients. Building on this theoretical foundation, we introduce unbiased variance reduction strategies, including optimal Monte Carlo budget allocation and antithetic sampling, that significantly improve the performance of MDM alignment. We demonstrate the effectiveness of VRPO by applying it to LLaDA, and the resulting model, LLaDA 1.5, outperforms its SFT-only predecessor consistently and significantly across mathematical (GSM8K +4.7), code (HumanEval +3.0, MBPP +1.8), and alignment benchmarks (IFEval +4.0, Arena-Hard +4.3). Furthermore, LLaDA 1.5 demonstrates a highly competitive mathematical performance compared to strong language MDMs and ARMs. Project page: https://ml-gsai.github.io/LLaDA-1.5-Demo/.

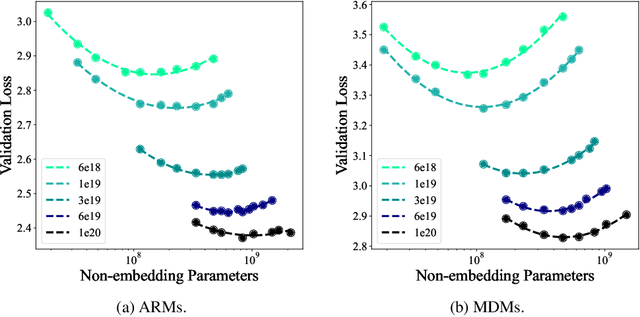
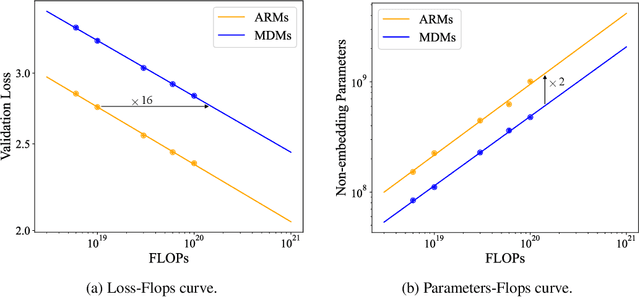
Scaling up Masked Diffusion Models on Text

Masked diffusion models (MDMs) have shown promise in language modeling, yet their scalability and effectiveness in core language tasks, such as text generation and language understanding, remain underexplored. This paper establishes the first scaling law for MDMs, demonstrating a scaling rate comparable to autoregressive models (ARMs) and a relatively small compute gap. Motivated by their scalability, we train a family of MDMs with up to 1.1 billion (B) parameters to systematically evaluate their performance against ARMs of comparable or larger sizes. Fully leveraging the probabilistic formulation of MDMs, we propose a simple yet effective \emph{unsupervised classifier-free guidance} that effectively exploits large-scale unpaired data, boosting performance for conditional inference. In language understanding, a 1.1B MDM shows competitive results, outperforming the larger 1.5B GPT-2 model on four out of eight zero-shot benchmarks. In text generation, MDMs provide a flexible trade-off compared to ARMs utilizing KV-cache: MDMs match the performance of ARMs while being 1.4 times faster, or achieve higher quality than ARMs at a higher computational cost. Moreover, MDMs address challenging tasks for ARMs by effectively handling bidirectional reasoning and adapting to temporal shifts in data. Notably, a 1.1B MDM breaks the \emph{reverse curse} encountered by much larger ARMs with significantly more data and computation, such as Llama-2 (13B) and GPT-3 (175B). Our code is available at \url{https://github.com/ML-GSAI/SMDM}.

Your Absorbing Discrete Diffusion Secretly Models the Conditional Distributions of Clean Data

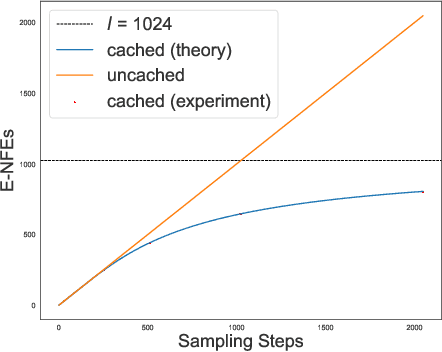
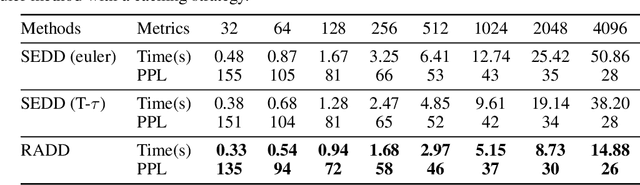
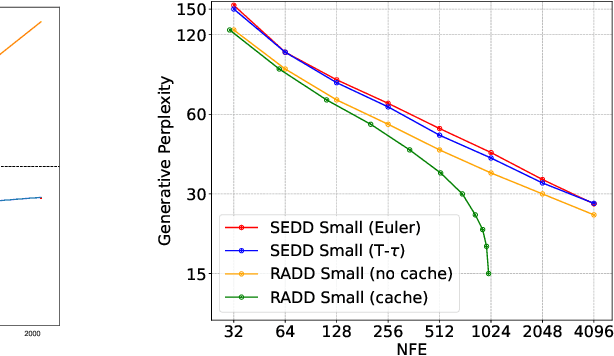
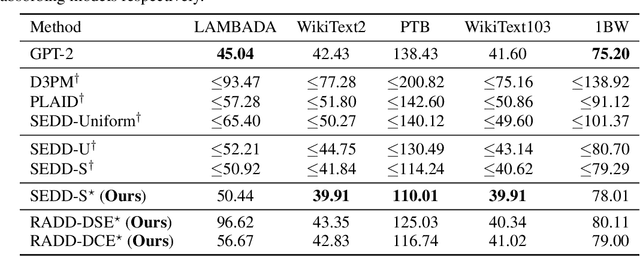
Discrete diffusion models with absorbing processes have shown promise in language modeling. The key quantities to be estimated are the ratios between the marginal probabilities of two transitive states at all timesteps, called the concrete score. In this paper, we reveal that the concrete score in absorbing diffusion can be expressed as conditional probabilities of clean data, multiplied by a time-dependent scalar in an analytic form. Motivated by the finding, we propose reparameterized absorbing discrete diffusion (RADD), a dedicated diffusion model that characterizes the time-independent conditional probabilities. Besides its simplicity, RADD can reduce the number of function evaluations (NFEs) by caching the output of the time-independent network when the noisy sample remains unchanged in a sampling interval. Empirically, RADD is up to 3.5 times faster while consistently achieving a better performance than the strongest baseline. Built upon the new factorization of the concrete score, we further prove a surprising result that the exact likelihood of absorbing diffusion can be rewritten to a simple form (named denoising cross-entropy) and then estimated efficiently by the Monte Carlo method. The resulting approach also applies to the original parameterization of the concrete score. It significantly advances the state-of-the-art discrete diffusion on 5 zero-shot language modeling benchmarks (measured by perplexity) at the GPT-2 scale.