Continuous Semi-Implicit Models

Semi-implicit distributions have shown great promise in variational inference and generative modeling. Hierarchical semi-implicit models, which stack multiple semi-implicit layers, enhance the expressiveness of semi-implicit distributions and can be used to accelerate diffusion models given pretrained score networks. However, their sequential training often suffers from slow convergence. In this paper, we introduce CoSIM, a continuous semi-implicit model that extends hierarchical semi-implicit models into a continuous framework. By incorporating a continuous transition kernel, CoSIM enables efficient, simulation-free training. Furthermore, we show that CoSIM achieves consistency with a carefully designed transition kernel, offering a novel approach for multistep distillation of generative models at the distributional level. Extensive experiments on image generation demonstrate that CoSIM performs on par or better than existing diffusion model acceleration methods, achieving superior performance on FD-DINOv2.

Variational Autoencoding Discrete Diffusion with Enhanced Dimensional Correlations Modeling

Discrete diffusion models have recently shown great promise for modeling complex discrete data, with masked diffusion models (MDMs) offering a compelling trade-off between quality and generation speed. MDMs denoise by progressively unmasking multiple dimensions from an all-masked input, but their performance can degrade when using few denoising steps due to limited modeling of inter-dimensional dependencies. In this paper, we propose Variational Autoencoding Discrete Diffusion (VADD), a novel framework that enhances discrete diffusion with latent variable modeling to implicitly capture correlations among dimensions. By introducing an auxiliary recognition model, VADD enables stable training via variational lower bounds maximization and amortized inference over the training set. Our approach retains the efficiency of traditional MDMs while significantly improving sample quality, especially when the number of denoising steps is small. Empirical results on 2D toy data, pixel-level image generation, and text generation demonstrate that VADD consistently outperforms MDM baselines.

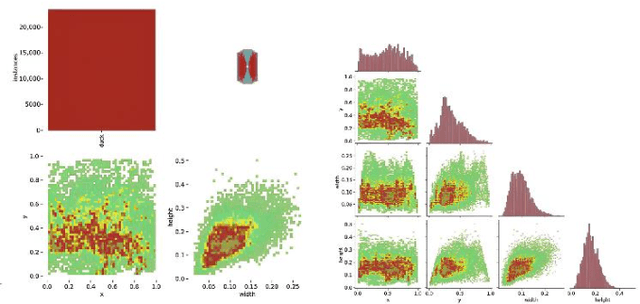
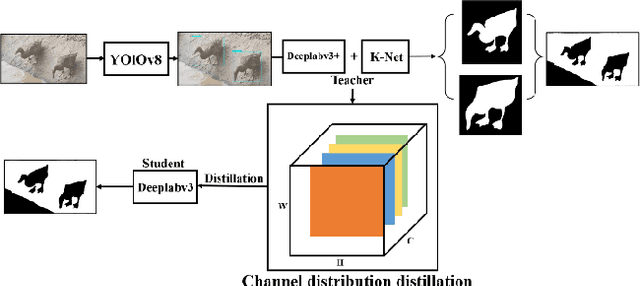
DuckSegmentation: A segmentation model based on the AnYue Hemp Duck Dataset

The modernization of smart farming is a way to improve agricultural production efficiency, and improve the agricultural production environment. Although many large models have achieved high accuracy in the task of object recognition and segmentation, they cannot really be put into use in the farming industry due to their own poor interpretability and limitations in computational volume. In this paper, we built AnYue Shelduck Dateset, which contains a total of 1951 Shelduck datasets, and performed target detection and segmentation annotation with the help of professional annotators. Based on AnYue ShelduckDateset, this paper describes DuckProcessing, an efficient and powerful module for duck identification based on real shelduckfarms. First of all, using the YOLOv8 module designed to divide the mahjong between them, Precision reached 98.10%, Recall reached 96.53% and F1 score reached 0.95 on the test set. Again using the DuckSegmentation segmentation model, DuckSegmentation reached 96.43% mIoU. Finally, the excellent DuckSegmentation was used as the teacher model, and through knowledge distillation, Deeplabv3 r50 was used as the student model, and the final student model achieved 94.49% mIoU on the test set. The method provides a new way of thinking in practical sisal duck smart farming.

PhyloVAE: Unsupervised Learning of Phylogenetic Trees via Variational Autoencoders

Learning informative representations of phylogenetic tree structures is essential for analyzing evolutionary relationships. Classical distance-based methods have been widely used to project phylogenetic trees into Euclidean space, but they are often sensitive to the choice of distance metric and may lack sufficient resolution. In this paper, we introduce phylogenetic variational autoencoders (PhyloVAEs), an unsupervised learning framework designed for representation learning and generative modeling of tree topologies. Leveraging an efficient encoding mechanism inspired by autoregressive tree topology generation, we develop a deep latent-variable generative model that facilitates fast, parallelized topology generation. PhyloVAE combines this generative model with a collaborative inference model based on learnable topological features, allowing for high-resolution representations of phylogenetic tree samples. Extensive experiments demonstrate PhyloVAE's robust representation learning capabilities and fast generation of phylogenetic tree topologies.

Provable Sample-Efficient Transfer Learning Conditional Diffusion Models via Representation Learning

While conditional diffusion models have achieved remarkable success in various applications, they require abundant data to train from scratch, which is often infeasible in practice. To address this issue, transfer learning has emerged as an essential paradigm in small data regimes. Despite its empirical success, the theoretical underpinnings of transfer learning conditional diffusion models remain unexplored. In this paper, we take the first step towards understanding the sample efficiency of transfer learning conditional diffusion models through the lens of representation learning. Inspired by practical training procedures, we assume that there exists a low-dimensional representation of conditions shared across all tasks. Our analysis shows that with a well-learned representation from source tasks, the samplecomplexity of target tasks can be reduced substantially. In addition, we investigate the practical implications of our theoretical results in several real-world applications of conditional diffusion models. Numerical experiments are also conducted to verify our results.

Diffusion-PINN Sampler

Recent success of diffusion models has inspired a surge of interest in developing sampling techniques using reverse diffusion processes. However, accurately estimating the drift term in the reverse stochastic differential equation (SDE) solely from the unnormalized target density poses significant challenges, hindering existing methods from achieving state-of-the-art performance. In this paper, we introduce the Diffusion-PINN Sampler (DPS), a novel diffusion-based sampling algorithm that estimates the drift term by solving the governing partial differential equation of the log-density of the underlying SDE marginals via physics-informed neural networks (PINN). We prove that the error of log-density approximation can be controlled by the PINN residual loss, enabling us to establish convergence guarantees of DPS. Experiments on a variety of sampling tasks demonstrate the effectiveness of our approach, particularly in accurately identifying mixing proportions when the target contains isolated components.

Improving Tree Probability Estimation with Stochastic Optimization and Variance Reduction

Probability estimation of tree topologies is one of the fundamental tasks in phylogenetic inference. The recently proposed subsplit Bayesian networks (SBNs) provide a powerful probabilistic graphical model for tree topology probability estimation by properly leveraging the hierarchical structure of phylogenetic trees. However, the expectation maximization (EM) method currently used for learning SBN parameters does not scale up to large data sets. In this paper, we introduce several computationally efficient methods for training SBNs and show that variance reduction could be the key for better performance. Furthermore, we also introduce the variance reduction technique to improve the optimization of SBN parameters for variational Bayesian phylogenetic inference (VBPI). Extensive synthetic and real data experiments demonstrate that our methods outperform previous baseline methods on the tasks of tree topology probability estimation as well as Bayesian phylogenetic inference using SBNs.

Variational Bayesian Phylogenetic Inference with Semi-implicit Branch Length Distributions

Reconstructing the evolutionary history relating a collection of molecular sequences is the main subject of modern Bayesian phylogenetic inference. However, the commonly used Markov chain Monte Carlo methods can be inefficient due to the complicated space of phylogenetic trees, especially when the number of sequences is large. An alternative approach is variational Bayesian phylogenetic inference (VBPI) which transforms the inference problem into an optimization problem. While effective, the default diagonal lognormal approximation for the branch lengths of the tree used in VBPI is often insufficient to capture the complexity of the exact posterior. In this work, we propose a more flexible family of branch length variational posteriors based on semi-implicit hierarchical distributions using graph neural networks. We show that this semi-implicit construction emits straightforward permutation equivariant distributions, and therefore can handle the non-Euclidean branch length space across different tree topologies with ease. To deal with the intractable marginal probability of semi-implicit variational distributions, we develop several alternative lower bounds for stochastic optimization. We demonstrate the effectiveness of our proposed method over baseline methods on benchmark data examples, in terms of both marginal likelihood estimation and branch length posterior approximation.

Kernel Semi-Implicit Variational Inference

Semi-implicit variational inference (SIVI) extends traditional variational families with semi-implicit distributions defined in a hierarchical manner. Due to the intractable densities of semi-implicit distributions, classical SIVI often resorts to surrogates of evidence lower bound (ELBO) that would introduce biases for training. A recent advancement in SIVI, named SIVI-SM, utilizes an alternative score matching objective made tractable via a minimax formulation, albeit requiring an additional lower-level optimization. In this paper, we propose kernel SIVI (KSIVI), a variant of SIVI-SM that eliminates the need for lower-level optimization through kernel tricks. Specifically, we show that when optimizing over a reproducing kernel Hilbert space (RKHS), the lower-level problem has an explicit solution. This way, the upper-level objective becomes the kernel Stein discrepancy (KSD), which is readily computable for stochastic gradient descent due to the hierarchical structure of semi-implicit variational distributions. An upper bound for the variance of the Monte Carlo gradient estimators of the KSD objective is derived, which allows us to establish novel convergence guarantees of KSIVI. We demonstrate the effectiveness and efficiency of KSIVI on both synthetic distributions and a variety of real data Bayesian inference tasks.

Reflected Flow Matching

Continuous normalizing flows (CNFs) learn an ordinary differential equation to transform prior samples into data. Flow matching (FM) has recently emerged as a simulation-free approach for training CNFs by regressing a velocity model towards the conditional velocity field. However, on constrained domains, the learned velocity model may lead to undesirable flows that result in highly unnatural samples, e.g., oversaturated images, due to both flow matching error and simulation error. To address this, we add a boundary constraint term to CNFs, which leads to reflected CNFs that keep trajectories within the constrained domains. We propose reflected flow matching (RFM) to train the velocity model in reflected CNFs by matching the conditional velocity fields in a simulation-free manner, similar to the vanilla FM. Moreover, the analytical form of conditional velocity fields in RFM avoids potentially biased approximations, making it superior to existing score-based generative models on constrained domains. We demonstrate that RFM achieves comparable or better results on standard image benchmarks and produces high-quality class-conditioned samples under high guidance weight.