Variational Bayesian Phylogenetic Inference with Semi-implicit Branch Length Distributions

Reconstructing the evolutionary history relating a collection of molecular sequences is the main subject of modern Bayesian phylogenetic inference. However, the commonly used Markov chain Monte Carlo methods can be inefficient due to the complicated space of phylogenetic trees, especially when the number of sequences is large. An alternative approach is variational Bayesian phylogenetic inference (VBPI) which transforms the inference problem into an optimization problem. While effective, the default diagonal lognormal approximation for the branch lengths of the tree used in VBPI is often insufficient to capture the complexity of the exact posterior. In this work, we propose a more flexible family of branch length variational posteriors based on semi-implicit hierarchical distributions using graph neural networks. We show that this semi-implicit construction emits straightforward permutation equivariant distributions, and therefore can handle the non-Euclidean branch length space across different tree topologies with ease. To deal with the intractable marginal probability of semi-implicit variational distributions, we develop several alternative lower bounds for stochastic optimization. We demonstrate the effectiveness of our proposed method over baseline methods on benchmark data examples, in terms of both marginal likelihood estimation and branch length posterior approximation.

A Variational Approach to Bayesian Phylogenetic Inference

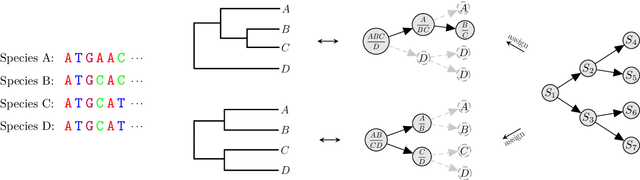
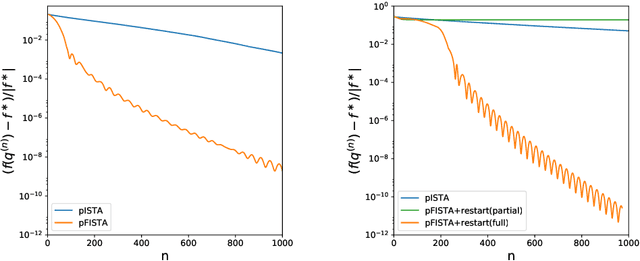
Bayesian phylogenetic inference is currently done via Markov chain Monte Carlo (MCMC) with simple proposal mechanisms. This hinders exploration efficiency and often requires long runs to deliver accurate posterior estimates. In this paper, we present an alternative approach: a variational framework for Bayesian phylogenetic analysis. We propose combining subsplit Bayesian networks, an expressive graphical model for tree topology distributions, and a structured amortization of the branch lengths over tree topologies for a suitable variational family of distributions. We train the variational approximation via stochastic gradient ascent and adopt gradient estimators for continuous and discrete variational parameters separately to deal with the composite latent space of phylogenetic models. We show that our variational approach provides competitive performance to MCMC, while requiring much less computation due to a more efficient exploration mechanism enabled by variational inference. Experiments on a benchmark of challenging real data Bayesian phylogenetic inference problems demonstrate the effectiveness and efficiency of our methods.

Non-bifurcating phylogenetic tree inference via the adaptive LASSO

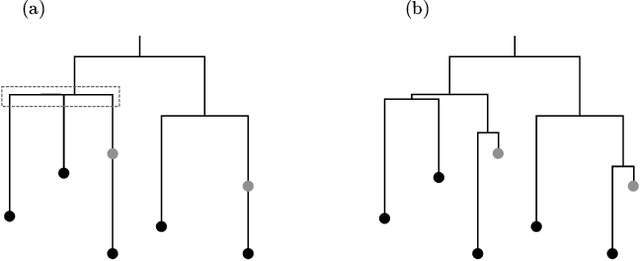
Phylogenetic tree inference using deep DNA sequencing is reshaping our understanding of rapidly evolving systems, such as the within-host battle between viruses and the immune system. Densely sampled phylogenetic trees can contain special features, including "sampled ancestors" in which we sequence a genotype along with its direct descendants, and "polytomies" in which multiple descendants arise simultaneously. These features are apparent after identifying zero-length branches in the tree. However, current maximum-likelihood based approaches are not capable of revealing such zero-length branches. In this paper, we find these zero-length branches by introducing adaptive-LASSO-type regularization estimators to phylogenetics, deriving their properties, and showing regularization to be a practically useful approach for phylogenetics.