QCQP-Net: Reliably Learning Feasible Alternating Current Optimal Power Flow Solutions Under Constraints

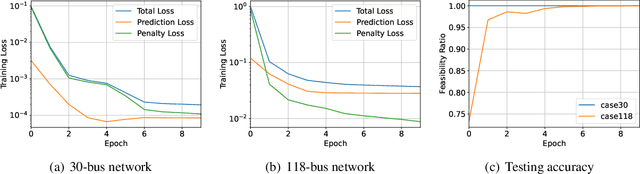
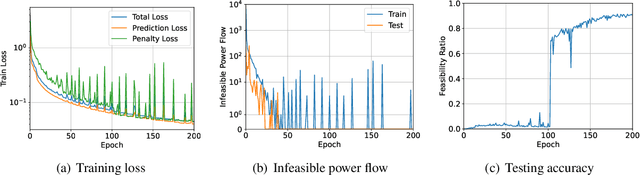
At the heart of power system operations, alternating current optimal power flow (ACOPF) studies the generation of electric power in the most economical way under network-wide load requirement, and can be formulated as a highly structured non-convex quadratically constrained quadratic program (QCQP). Optimization-based solutions to ACOPF (such as ADMM or interior-point method), as the classic approach, require large amount of computation and cannot meet the need to repeatedly solve the problem as load requirement frequently changes. On the other hand, learning-based methods that directly predict the ACOPF solution given the load input incur little computational cost but often generates infeasible solutions (i.e. violate the constraints of ACOPF). In this work, we combine the best of both worlds -- we propose an innovated framework for learning ACOPF, where the input load is mapped to the ACOPF solution through a neural network in a computationally efficient and reliable manner. Key to our innovation is a specific-purpose "activation function" defined implicitly by a QCQP and a novel loss, which enforce constraint satisfaction. We show through numerical simulations that our proposed method achieves superior feasibility rate and generation cost in situations where the existing learning-based approaches fail.

APPFL: Open-Source Software Framework for Privacy-Preserving Federated Learning

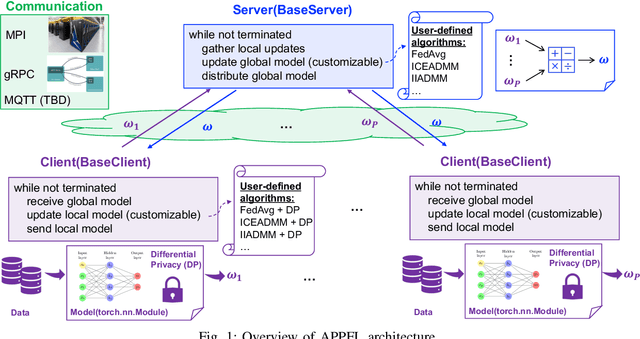
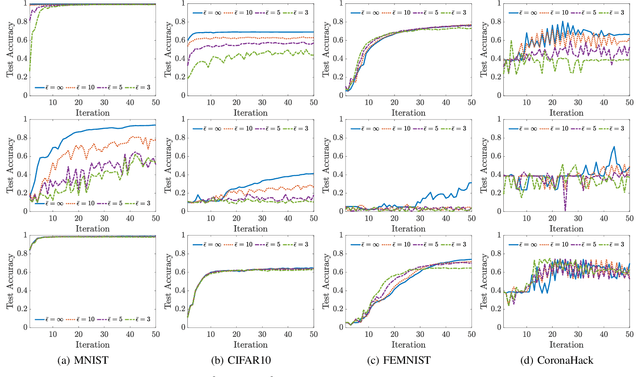
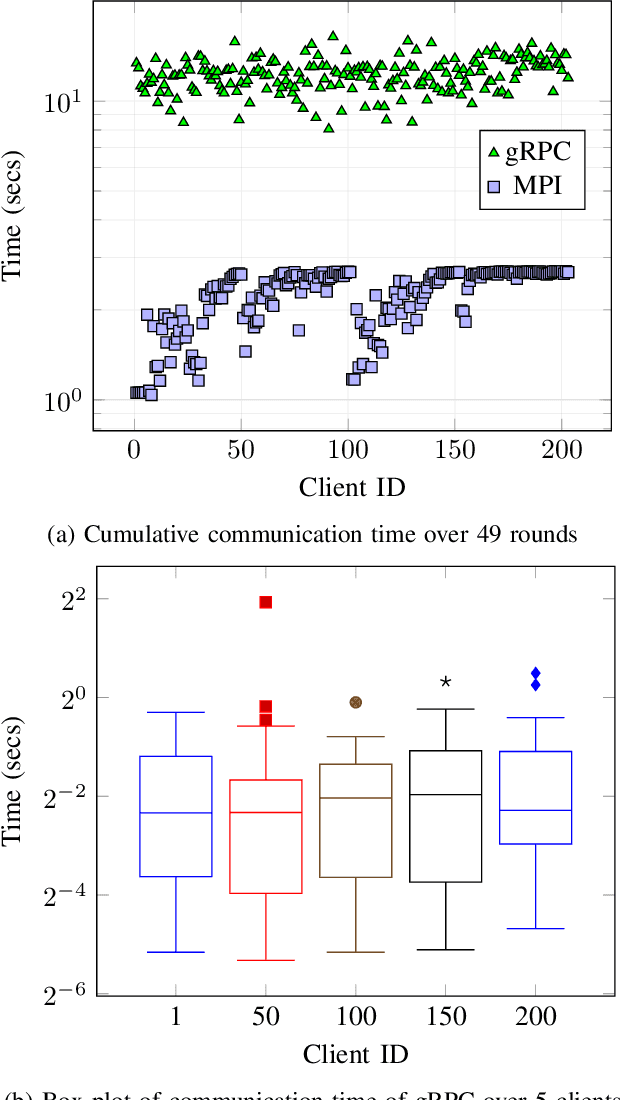
Federated learning (FL) enables training models at different sites and updating the weights from the training instead of transferring data to a central location and training as in classical machine learning. The FL capability is especially important to domains such as biomedicine and smart grid, where data may not be shared freely or stored at a central location because of policy challenges. Thanks to the capability of learning from decentralized datasets, FL is now a rapidly growing research field, and numerous FL frameworks have been developed. In this work, we introduce APPFL, the Argonne Privacy-Preserving Federated Learning framework. APPFL allows users to leverage implemented privacy-preserving algorithms, implement new algorithms, and simulate and deploy various FL algorithms with privacy-preserving techniques. The modular framework enables users to customize the components for algorithms, privacy, communication protocols, neural network models, and user data. We also present a new communication-efficient algorithm based on an inexact alternating direction method of multipliers. The algorithm requires significantly less communication between the server and the clients than does the current state of the art. We demonstrate the computational capabilities of APPFL, including differentially private FL on various test datasets and its scalability, by using multiple algorithms and datasets on different computing environments.

A Reinforcement Learning Approach to Parameter Selection for Distributed Optimization in Power Systems

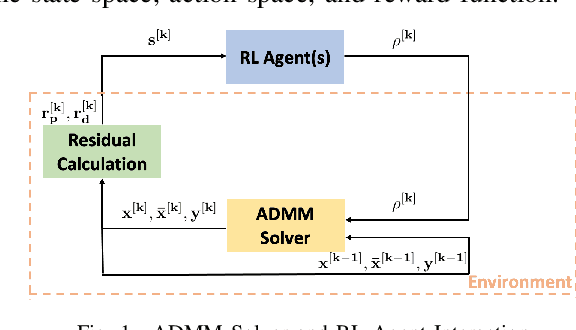
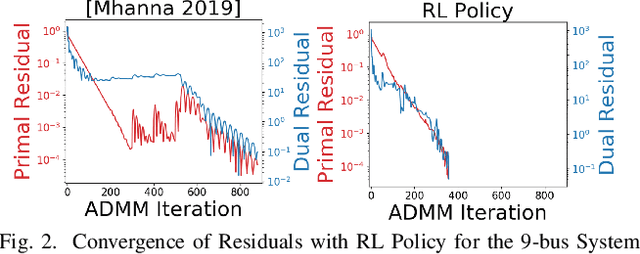
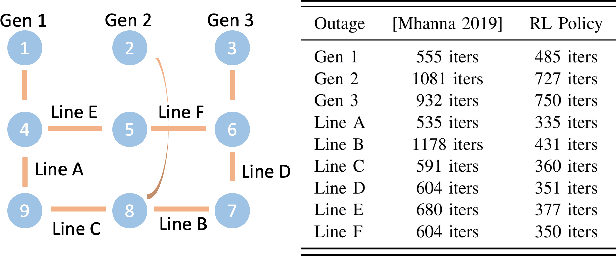
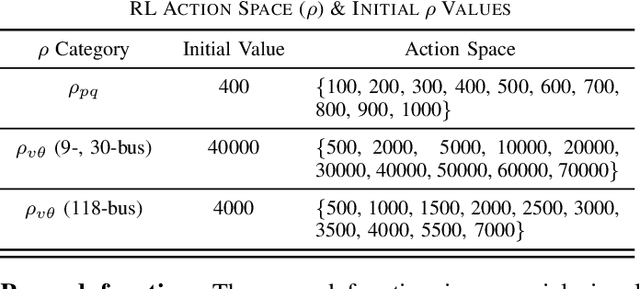
With the increasing penetration of distributed energy resources, distributed optimization algorithms have attracted significant attention for power systems applications due to their potential for superior scalability, privacy, and robustness to a single point-of-failure. The Alternating Direction Method of Multipliers (ADMM) is a popular distributed optimization algorithm; however, its convergence performance is highly dependent on the selection of penalty parameters, which are usually chosen heuristically. In this work, we use reinforcement learning (RL) to develop an adaptive penalty parameter selection policy for the AC optimal power flow (ACOPF) problem solved via ADMM with the goal of minimizing the number of iterations until convergence. We train our RL policy using deep Q-learning, and show that this policy can result in significantly accelerated convergence (up to a 59% reduction in the number of iterations compared to existing, curvature-informed penalty parameter selection methods). Furthermore, we show that our RL policy demonstrates promise for generalizability, performing well under unseen loading schemes as well as under unseen losses of lines and generators (up to a 50% reduction in iterations). This work thus provides a proof-of-concept for using RL for parameter selection in ADMM for power systems applications.