Hard Constraint Guided Flow Matching for Gradient-Free Generation of PDE Solutions

Generative models that satisfy hard constraints are crucial in many scientific and engineering applications where physical laws or system requirements must be strictly respected. However, many existing constrained generative models, especially those developed for computer vision, rely heavily on gradient information, often sparse or computationally expensive in fields like partial differential equations (PDEs). In this work, we introduce a novel framework for adapting pre-trained, unconstrained flow-matching models to satisfy constraints exactly in a zero-shot manner without requiring expensive gradient computations or fine-tuning. Our framework, ECI sampling, alternates between extrapolation (E), correction (C), and interpolation (I) stages during each iterative sampling step of flow matching sampling to ensure accurate integration of constraint information while preserving the validity of the generation. We demonstrate the effectiveness of our approach across various PDE systems, showing that ECI-guided generation strictly adheres to physical constraints and accurately captures complex distribution shifts induced by these constraints. Empirical results demonstrate that our framework consistently outperforms baseline approaches in various zero-shot constrained generation tasks and also achieves competitive results in the regression tasks without additional fine-tuning.

Hotspot-Driven Peptide Design via Multi-Fragment Autoregressive Extension

Peptides, short chains of amino acids, interact with target proteins, making them a unique class of protein-based therapeutics for treating human diseases. Recently, deep generative models have shown great promise in peptide generation. However, several challenges remain in designing effective peptide binders. First, not all residues contribute equally to peptide-target interactions. Second, the generated peptides must adopt valid geometries due to the constraints of peptide bonds. Third, realistic tasks for peptide drug development are still lacking. To address these challenges, we introduce PepHAR, a hot-spot-driven autoregressive generative model for designing peptides targeting specific proteins. Building on the observation that certain hot spot residues have higher interaction potentials, we first use an energy-based density model to fit and sample these key residues. Next, to ensure proper peptide geometry, we autoregressively extend peptide fragments by estimating dihedral angles between residue frames. Finally, we apply an optimization process to iteratively refine fragment assembly, ensuring correct peptide structures. By combining hot spot sampling with fragment-based extension, our approach enables de novo peptide design tailored to a target protein and allows the incorporation of key hot spot residues into peptide scaffolds. Extensive experiments, including peptide design and peptide scaffold generation, demonstrate the strong potential of PepHAR in computational peptide binder design.

Geometric Point Attention Transformer for 3D Shape Reassembly

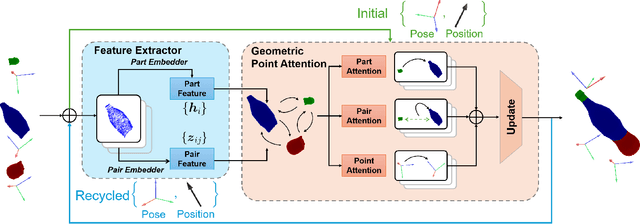
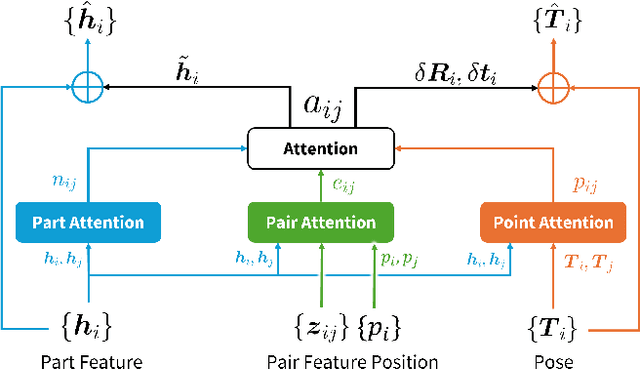
Shape assembly, which aims to reassemble separate parts into a complete object, has gained significant interest in recent years. Existing methods primarily rely on networks to predict the poses of individual parts, but often fail to effectively capture the geometric interactions between the parts and their poses. In this paper, we present the Geometric Point Attention Transformer (GPAT), a network specifically designed to address the challenges of reasoning about geometric relationships. In the geometric point attention module, we integrate both global shape information and local pairwise geometric features, along with poses represented as rotation and translation vectors for each part. To enable iterative updates and dynamic reasoning, we introduce a geometric recycling scheme, where each prediction is fed into the next iteration for refinement. We evaluate our model on both the semantic and geometric assembly tasks, showing that it outperforms previous methods in absolute pose estimation, achieving accurate pose predictions and high alignment accuracy.

Training Free Guided Flow Matching with Optimal Control

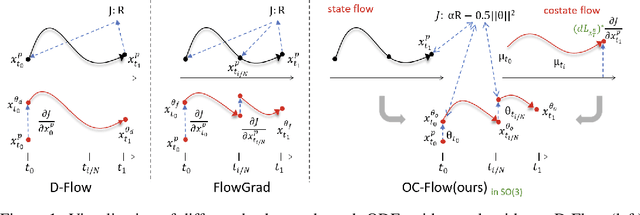
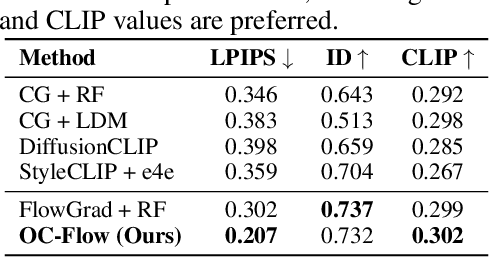
Controlled generation with pre-trained Diffusion and Flow Matching models has vast applications. One strategy for guiding ODE-based generative models is through optimizing a target loss $R(x_1)$ while staying close to the prior distribution. Along this line, some recent work showed the effectiveness of guiding flow model by differentiating through its ODE sampling process. Despite the superior performance, the theoretical understanding of this line of methods is still preliminary, leaving space for algorithm improvement. Moreover, existing methods predominately focus on Euclidean data manifold, and there is a compelling need for guided flow methods on complex geometries such as SO(3), which prevails in high-stake scientific applications like protein design. We present OC-Flow, a general and theoretically grounded training-free framework for guided flow matching using optimal control. Building upon advances in optimal control theory, we develop effective and practical algorithms for solving optimal control in guided ODE-based generation and provide a systematic theoretical analysis of the convergence guarantee in both Euclidean and SO(3). We show that existing backprop-through-ODE methods can be interpreted as special cases of Euclidean OC-Flow. OC-Flow achieved superior performance in extensive experiments on text-guided image manipulation, conditional molecule generation, and all-atom peptide design.

Neural P$^3$M: A Long-Range Interaction Modeling Enhancer for Geometric GNNs

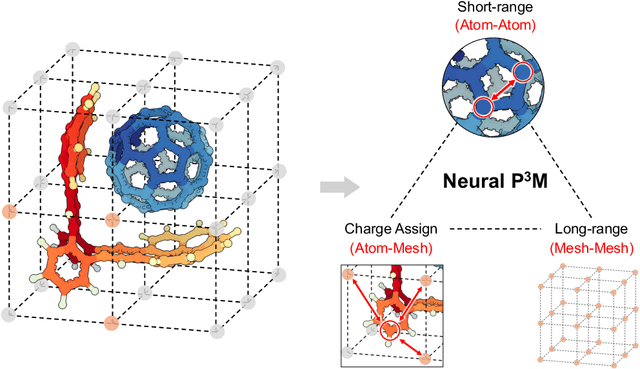
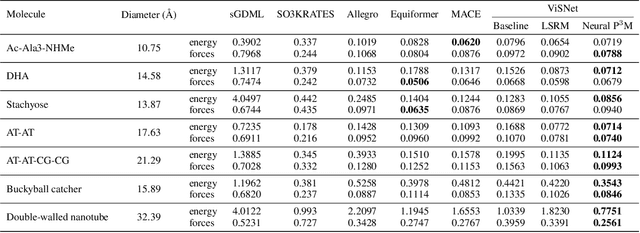
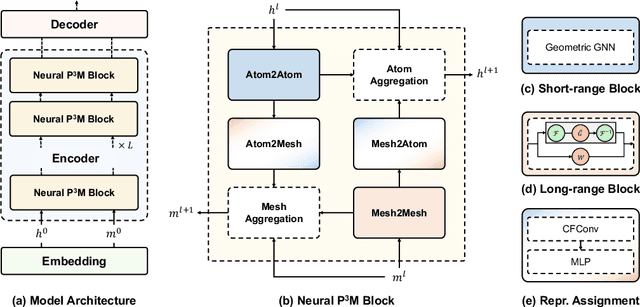
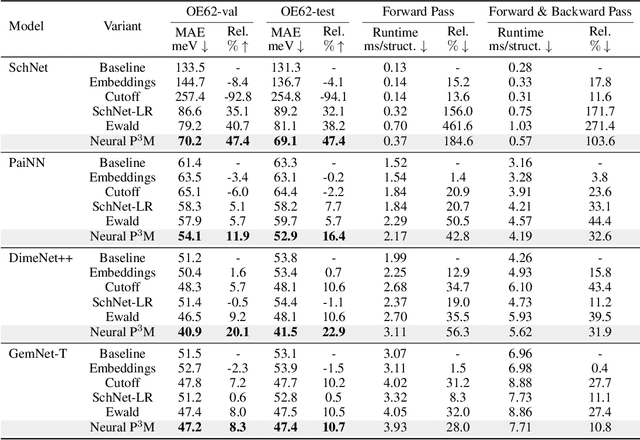
Geometric graph neural networks (GNNs) have emerged as powerful tools for modeling molecular geometry. However, they encounter limitations in effectively capturing long-range interactions in large molecular systems. To address this challenge, we introduce Neural P$^3$M, a versatile enhancer of geometric GNNs to expand the scope of their capabilities by incorporating mesh points alongside atoms and reimaging traditional mathematical operations in a trainable manner. Neural P$^3$M exhibits flexibility across a wide range of molecular systems and demonstrates remarkable accuracy in predicting energies and forces, outperforming on benchmarks such as the MD22 dataset. It also achieves an average improvement of 22% on the OE62 dataset while integrating with various architectures.

Full-Atom Peptide Design based on Multi-modal Flow Matching

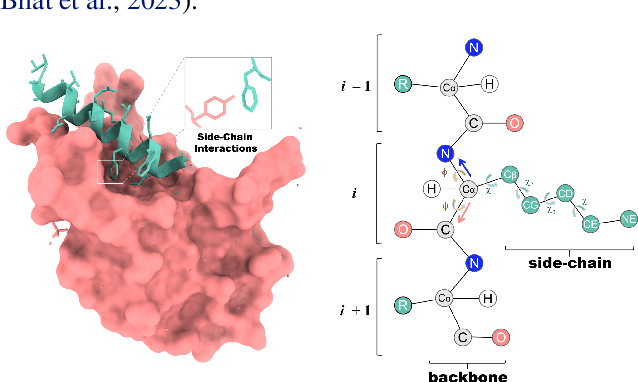
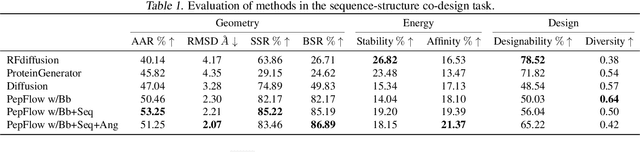
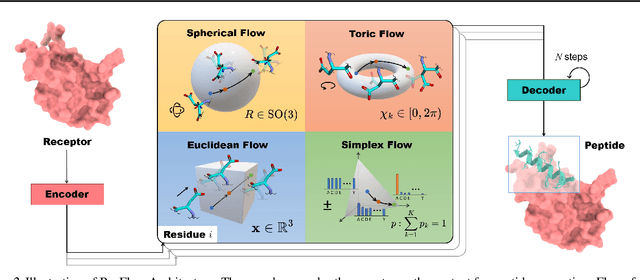
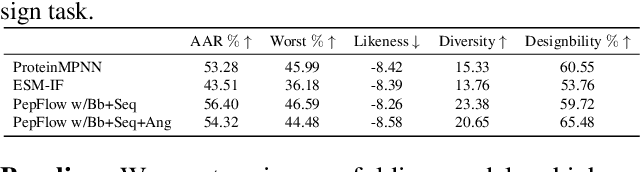
Peptides, short chains of amino acid residues, play a vital role in numerous biological processes by interacting with other target molecules, offering substantial potential in drug discovery. In this work, we present PepFlow, the first multi-modal deep generative model grounded in the flow-matching framework for the design of full-atom peptides that target specific protein receptors. Drawing inspiration from the crucial roles of residue backbone orientations and side-chain dynamics in protein-peptide interactions, we characterize the peptide structure using rigid backbone frames within the $\mathrm{SE}(3)$ manifold and side-chain angles on high-dimensional tori. Furthermore, we represent discrete residue types in the peptide sequence as categorical distributions on the probability simplex. By learning the joint distributions of each modality using derived flows and vector fields on corresponding manifolds, our method excels in the fine-grained design of full-atom peptides. Harnessing the multi-modal paradigm, our approach adeptly tackles various tasks such as fix-backbone sequence design and side-chain packing through partial sampling. Through meticulously crafted experiments, we demonstrate that PepFlow exhibits superior performance in comprehensive benchmarks, highlighting its significant potential in computational peptide design and analysis.

Categorical Flow Matching on Statistical Manifolds

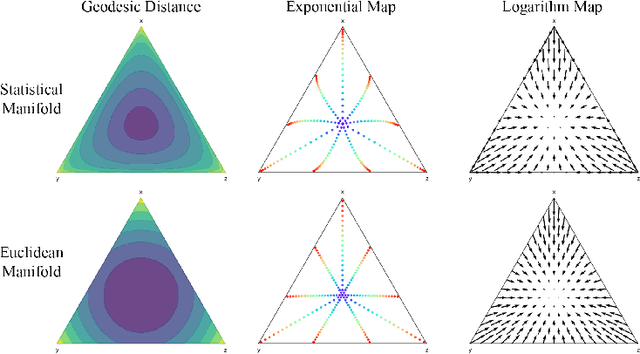
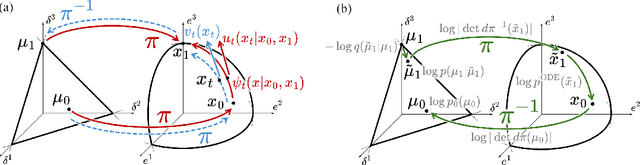
We introduce Statistical Flow Matching (SFM), a novel and mathematically rigorous flow-matching framework on the manifold of parameterized probability measures inspired by the results from information geometry. We demonstrate the effectiveness of our method on the discrete generation problem by instantiating SFM on the manifold of categorical distributions whose geometric properties remain unexplored in previous discrete generative models. Utilizing the Fisher information metric, we equip the manifold with a Riemannian structure whose intrinsic geometries are effectively leveraged by following the shortest paths of geodesics. We develop an efficient training and sampling algorithm that overcomes numerical stability issues with a diffeomorphism between manifolds. Our distinctive geometric perspective of statistical manifolds allows us to apply optimal transport during training and interpret SFM as following the steepest direction of the natural gradient. Unlike previous models that rely on variational bounds for likelihood estimation, SFM enjoys the exact likelihood calculation for arbitrary probability measures. We manifest that SFM can learn more complex patterns on the statistical manifold where existing models often fail due to strong prior assumptions. Comprehensive experiments on real-world generative tasks ranging from image, text to biological domains further demonstrate that SFM achieves higher sampling quality and likelihood than other discrete diffusion or flow-based models.

Equivariant Neural Operator Learning with Graphon Convolution

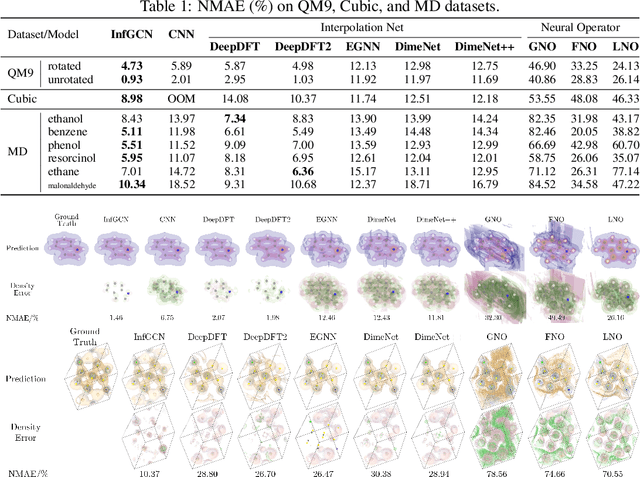
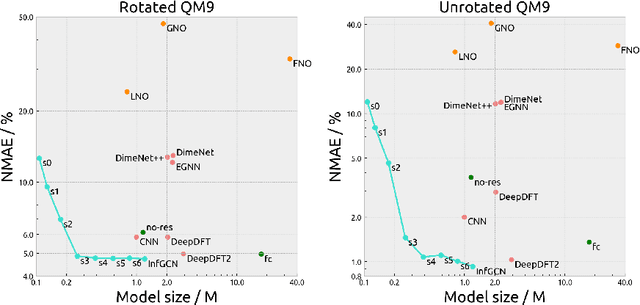
We propose a general architecture that combines the coefficient learning scheme with a residual operator layer for learning mappings between continuous functions in the 3D Euclidean space. Our proposed model is guaranteed to achieve SE(3)-equivariance by design. From the graph spectrum view, our method can be interpreted as convolution on graphons (dense graphs with infinitely many nodes), which we term InfGCN. By leveraging both the continuous graphon structure and the discrete graph structure of the input data, our model can effectively capture the geometric information while preserving equivariance. Through extensive experiments on large-scale electron density datasets, we observed that our model significantly outperformed the current state-of-the-art architectures. Multiple ablation studies were also carried out to demonstrate the effectiveness of the proposed architecture.

Equivariant Point Cloud Analysis via Learning Orientations for Message Passing

Equivariance has been a long-standing concern in various fields ranging from computer vision to physical modeling. Most previous methods struggle with generality, simplicity, and expressiveness -- some are designed ad hoc for specific data types, some are too complex to be accessible, and some sacrifice flexible transformations. In this work, we propose a novel and simple framework to achieve equivariance for point cloud analysis based on the message passing (graph neural network) scheme. We find the equivariant property could be obtained by introducing an orientation for each point to decouple the relative position for each point from the global pose of the entire point cloud. Therefore, we extend current message passing networks with a module that learns orientations for each point. Before aggregating information from the neighbors of a point, the networks transforms the neighbors' coordinates based on the point's learned orientations. We provide formal proofs to show the equivariance of the proposed framework. Empirically, we demonstrate that our proposed method is competitive on both point cloud analysis and physical modeling tasks. Code is available at https://github.com/luost26/Equivariant-OrientedMP .

Directed Weight Neural Networks for Protein Structure Representation Learning

A protein performs biological functions by folding to a particular 3D structure. To accurately model the protein structures, both the overall geometric topology and local fine-grained relations between amino acids (e.g. side-chain torsion angles and inter-amino-acid orientations) should be carefully considered. In this work, we propose the Directed Weight Neural Network for better capturing geometric relations among different amino acids. Extending a single weight from a scalar to a 3D directed vector, our new framework supports a rich set of geometric operations on both classical and SO(3)--representation features, on top of which we construct a perceptron unit for processing amino-acid information. In addition, we introduce an equivariant message passing paradigm on proteins for plugging the directed weight perceptrons into existing Graph Neural Networks, showing superior versatility in maintaining SO(3)-equivariance at the global scale. Experiments show that our network has remarkably better expressiveness in representing geometric relations in comparison to classical neural networks and the (globally) equivariant networks. It also achieves state-of-the-art performance on various computational biology applications related to protein 3D structures.