Equivariant Neural Operator Learning with Graphon Convolution
Paper and Code
Nov 17, 2023
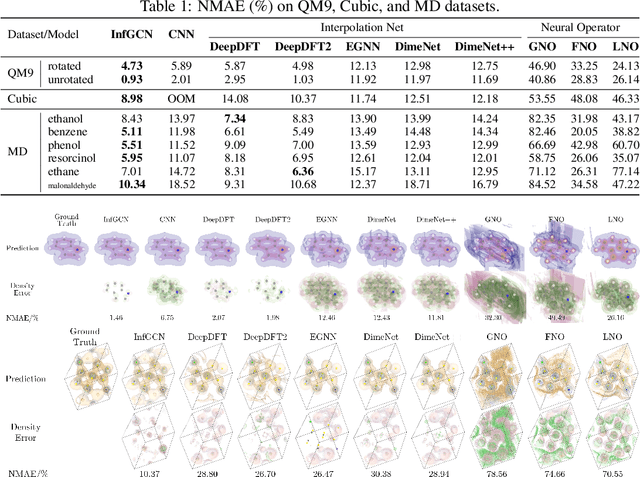

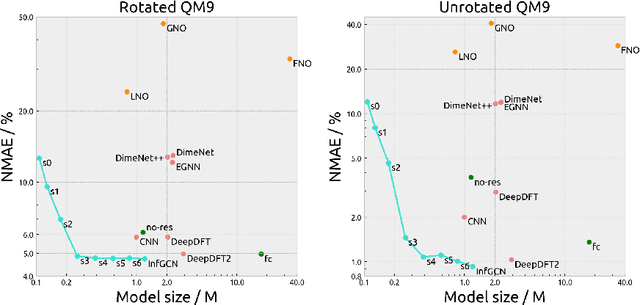
We propose a general architecture that combines the coefficient learning scheme with a residual operator layer for learning mappings between continuous functions in the 3D Euclidean space. Our proposed model is guaranteed to achieve SE(3)-equivariance by design. From the graph spectrum view, our method can be interpreted as convolution on graphons (dense graphs with infinitely many nodes), which we term InfGCN. By leveraging both the continuous graphon structure and the discrete graph structure of the input data, our model can effectively capture the geometric information while preserving equivariance. Through extensive experiments on large-scale electron density datasets, we observed that our model significantly outperformed the current state-of-the-art architectures. Multiple ablation studies were also carried out to demonstrate the effectiveness of the proposed architecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge