Full-Atom Peptide Design based on Multi-modal Flow Matching

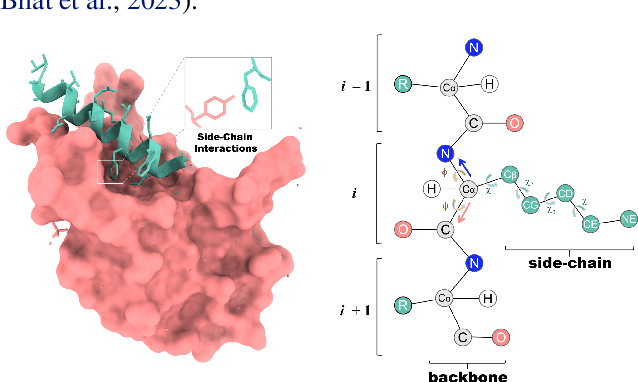
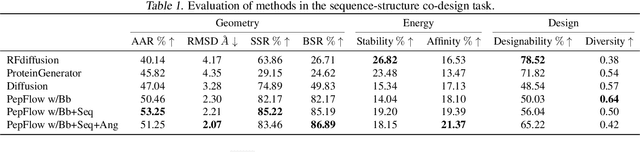
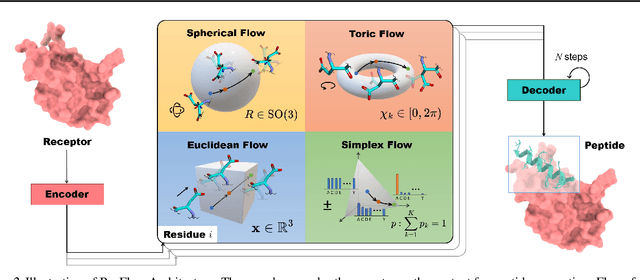
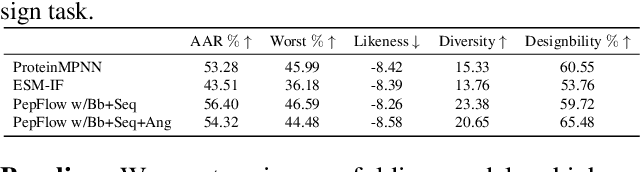
Peptides, short chains of amino acid residues, play a vital role in numerous biological processes by interacting with other target molecules, offering substantial potential in drug discovery. In this work, we present PepFlow, the first multi-modal deep generative model grounded in the flow-matching framework for the design of full-atom peptides that target specific protein receptors. Drawing inspiration from the crucial roles of residue backbone orientations and side-chain dynamics in protein-peptide interactions, we characterize the peptide structure using rigid backbone frames within the $\mathrm{SE}(3)$ manifold and side-chain angles on high-dimensional tori. Furthermore, we represent discrete residue types in the peptide sequence as categorical distributions on the probability simplex. By learning the joint distributions of each modality using derived flows and vector fields on corresponding manifolds, our method excels in the fine-grained design of full-atom peptides. Harnessing the multi-modal paradigm, our approach adeptly tackles various tasks such as fix-backbone sequence design and side-chain packing through partial sampling. Through meticulously crafted experiments, we demonstrate that PepFlow exhibits superior performance in comprehensive benchmarks, highlighting its significant potential in computational peptide design and analysis.

Off-Policy Reinforcement Learning with Delayed Rewards

We study deep reinforcement learning (RL) algorithms with delayed rewards. In many real-world tasks, instant rewards are often not readily accessible or even defined immediately after the agent performs actions. In this work, we first formally define the environment with delayed rewards and discuss the challenges raised due to the non-Markovian nature of such environments. Then, we introduce a general off-policy RL framework with a new Q-function formulation that can handle the delayed rewards with theoretical convergence guarantees. For practical tasks with high dimensional state spaces, we further introduce the HC-decomposition rule of the Q-function in our framework which naturally leads to an approximation scheme that helps boost the training efficiency and stability. We finally conduct extensive experiments to demonstrate the superior performance of our algorithms over the existing work and their variants.