M3: High-fidelity Text-to-Image Generation via Multi-Modal, Multi-Agent and Multi-Round Visual Reasoning

Generative models have achieved impressive fidelity in text-to-image synthesis, yet struggle with complex compositional prompts involving multiple constraints. We introduce \textbf{M3 (Multi-Modal, Multi-Agent, Multi-Round)}, a training-free framework that systematically resolves these failures through iterative inference-time refinement. M3 orchestrates off-the-shelf foundation models in a robust multi-agent loop: a Planner decomposes prompts into verifiable checklists, while specialized Checker, Refiner, and Editor agents surgically correct constraints one at a time, with a Verifier ensuring monotonic improvement. Applied to open-source models, M3 achieves remarkable results on the challenging OneIG-EN benchmark, with our Qwen-Image+M3 surpassing commercial flagship systems including Imagen4 (0.515) and Seedream 3.0 (0.530), reaching state-of-the-art performance (0.532 overall). This demonstrates that intelligent multi-agent reasoning can elevate open-source models beyond proprietary alternatives. M3 also substantially improves GenEval compositional metrics, effectively doubling spatial reasoning performance on hardened test sets. As a plug-and-play module compatible with any pre-trained T2I model, M3 establishes a new paradigm for compositional generation without costly retraining.

ProteinZero: Self-Improving Protein Generation via Online Reinforcement Learning

Protein generative models have shown remarkable promise in protein design but still face limitations in success rate, due to the scarcity of high-quality protein datasets for supervised pretraining. We present ProteinZero, a novel framework that enables scalable, automated, and continuous self-improvement of the inverse folding model through online reinforcement learning. To achieve computationally tractable online feedback, we introduce efficient proxy reward models based on ESM-fold and a novel rapid ddG predictor that significantly accelerates evaluation speed. ProteinZero employs a general RL framework balancing multi-reward maximization, KL-divergence from a reference model, and a novel protein-embedding level diversity regularization that prevents mode collapse while promoting higher sequence diversity. Through extensive experiments, we demonstrate that ProteinZero substantially outperforms existing methods across every key metric in protein design, achieving significant improvements in structural accuracy, designability, thermodynamic stability, and sequence diversity. Most impressively, ProteinZero reduces design failure rates by approximately 36% - 48% compared to widely-used methods like ProteinMPNN, ESM-IF and InstructPLM, consistently achieving success rates exceeding 90% across diverse and complex protein folds. Notably, the entire RL run on CATH-4.3 can be done with a single 8 X GPU node in under 3 days, including reward computation. Our work establishes a new paradigm for protein design where models evolve continuously from their own generated outputs, opening new possibilities for exploring the vast protein design space.

Hotspot-Driven Peptide Design via Multi-Fragment Autoregressive Extension

Peptides, short chains of amino acids, interact with target proteins, making them a unique class of protein-based therapeutics for treating human diseases. Recently, deep generative models have shown great promise in peptide generation. However, several challenges remain in designing effective peptide binders. First, not all residues contribute equally to peptide-target interactions. Second, the generated peptides must adopt valid geometries due to the constraints of peptide bonds. Third, realistic tasks for peptide drug development are still lacking. To address these challenges, we introduce PepHAR, a hot-spot-driven autoregressive generative model for designing peptides targeting specific proteins. Building on the observation that certain hot spot residues have higher interaction potentials, we first use an energy-based density model to fit and sample these key residues. Next, to ensure proper peptide geometry, we autoregressively extend peptide fragments by estimating dihedral angles between residue frames. Finally, we apply an optimization process to iteratively refine fragment assembly, ensuring correct peptide structures. By combining hot spot sampling with fragment-based extension, our approach enables de novo peptide design tailored to a target protein and allows the incorporation of key hot spot residues into peptide scaffolds. Extensive experiments, including peptide design and peptide scaffold generation, demonstrate the strong potential of PepHAR in computational peptide binder design.

FAFE: Immune Complex Modeling with Geodesic Distance Loss on Noisy Group Frames

Despite the striking success of general protein folding models such as AlphaFold2(AF2, Jumper et al. (2021)), the accurate computational modeling of antibody-antigen complexes remains a challenging task. In this paper, we first analyze AF2's primary loss function, known as the Frame Aligned Point Error (FAPE), and raise a previously overlooked issue that FAPE tends to face gradient vanishing problem on high-rotational-error targets. To address this fundamental limitation, we propose a novel geodesic loss called Frame Aligned Frame Error (FAFE, denoted as F2E to distinguish from FAPE), which enables the model to better optimize both the rotational and translational errors between two frames. We then prove that F2E can be reformulated as a group-aware geodesic loss, which translates the optimization of the residue-to-residue error to optimizing group-to-group geodesic frame distance. By fine-tuning AF2 with our proposed new loss function, we attain a correct rate of 52.3\% (DockQ $>$ 0.23) on an evaluation set and 43.8\% correct rate on a subset with low homology, with substantial improvement over AF2 by 182\% and 100\% respectively.

Full-Atom Peptide Design based on Multi-modal Flow Matching

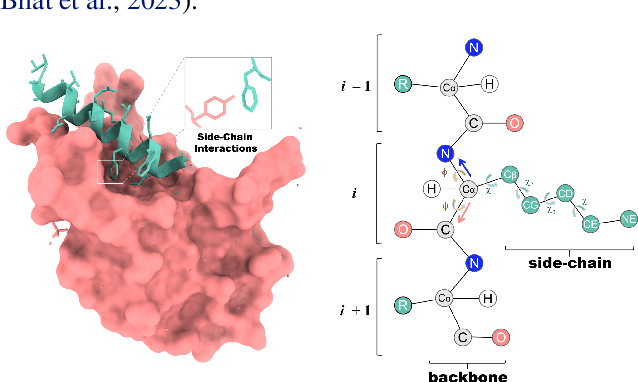
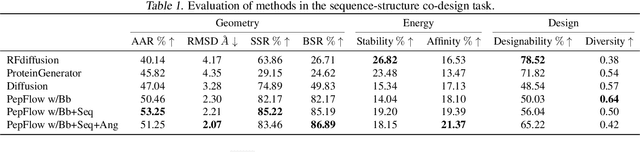
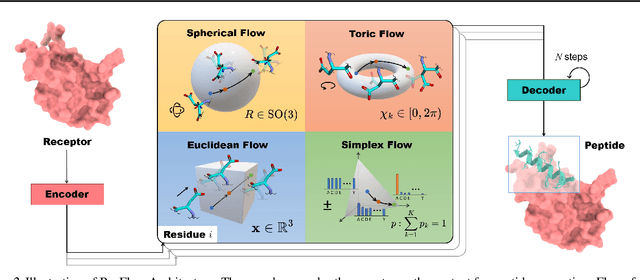
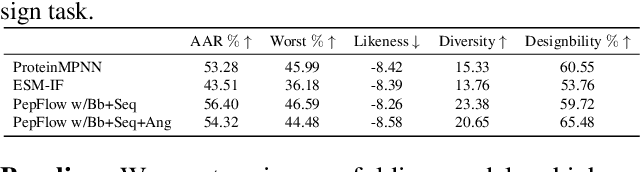
Peptides, short chains of amino acid residues, play a vital role in numerous biological processes by interacting with other target molecules, offering substantial potential in drug discovery. In this work, we present PepFlow, the first multi-modal deep generative model grounded in the flow-matching framework for the design of full-atom peptides that target specific protein receptors. Drawing inspiration from the crucial roles of residue backbone orientations and side-chain dynamics in protein-peptide interactions, we characterize the peptide structure using rigid backbone frames within the $\mathrm{SE}(3)$ manifold and side-chain angles on high-dimensional tori. Furthermore, we represent discrete residue types in the peptide sequence as categorical distributions on the probability simplex. By learning the joint distributions of each modality using derived flows and vector fields on corresponding manifolds, our method excels in the fine-grained design of full-atom peptides. Harnessing the multi-modal paradigm, our approach adeptly tackles various tasks such as fix-backbone sequence design and side-chain packing through partial sampling. Through meticulously crafted experiments, we demonstrate that PepFlow exhibits superior performance in comprehensive benchmarks, highlighting its significant potential in computational peptide design and analysis.

Learning Long-Term Reward Redistribution via Randomized Return Decomposition

Many practical applications of reinforcement learning require agents to learn from sparse and delayed rewards. It challenges the ability of agents to attribute their actions to future outcomes. In this paper, we consider the problem formulation of episodic reinforcement learning with trajectory feedback. It refers to an extreme delay of reward signals, in which the agent can only obtain one reward signal at the end of each trajectory. A popular paradigm for this problem setting is learning with a designed auxiliary dense reward function, namely proxy reward, instead of sparse environmental signals. Based on this framework, this paper proposes a novel reward redistribution algorithm, randomized return decomposition (RRD), to learn a proxy reward function for episodic reinforcement learning. We establish a surrogate problem by Monte-Carlo sampling that scales up least-squares-based reward redistribution to long-horizon problems. We analyze our surrogate loss function by connection with existing methods in the literature, which illustrates the algorithmic properties of our approach. In experiments, we extensively evaluate our proposed method on a variety of benchmark tasks with episodic rewards and demonstrate substantial improvement over baseline algorithms.