Categorical Flow Matching on Statistical Manifolds
Paper and Code
May 26, 2024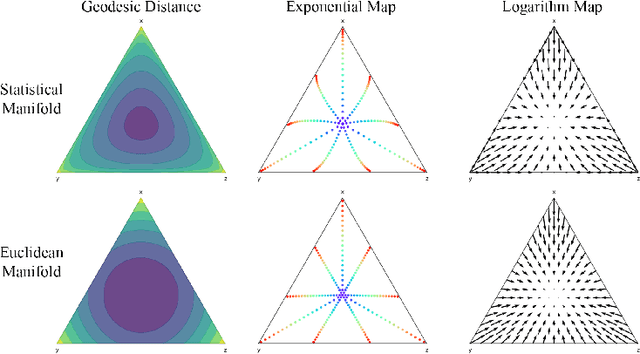

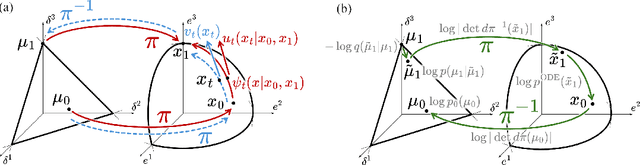

We introduce Statistical Flow Matching (SFM), a novel and mathematically rigorous flow-matching framework on the manifold of parameterized probability measures inspired by the results from information geometry. We demonstrate the effectiveness of our method on the discrete generation problem by instantiating SFM on the manifold of categorical distributions whose geometric properties remain unexplored in previous discrete generative models. Utilizing the Fisher information metric, we equip the manifold with a Riemannian structure whose intrinsic geometries are effectively leveraged by following the shortest paths of geodesics. We develop an efficient training and sampling algorithm that overcomes numerical stability issues with a diffeomorphism between manifolds. Our distinctive geometric perspective of statistical manifolds allows us to apply optimal transport during training and interpret SFM as following the steepest direction of the natural gradient. Unlike previous models that rely on variational bounds for likelihood estimation, SFM enjoys the exact likelihood calculation for arbitrary probability measures. We manifest that SFM can learn more complex patterns on the statistical manifold where existing models often fail due to strong prior assumptions. Comprehensive experiments on real-world generative tasks ranging from image, text to biological domains further demonstrate that SFM achieves higher sampling quality and likelihood than other discrete diffusion or flow-based models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge