An Experimental Design Framework for Label-Efficient Supervised Finetuning of Large Language Models

Supervised finetuning (SFT) on instruction datasets has played a crucial role in achieving the remarkable zero-shot generalization capabilities observed in modern large language models (LLMs). However, the annotation efforts required to produce high quality responses for instructions are becoming prohibitively expensive, especially as the number of tasks spanned by instruction datasets continues to increase. Active learning is effective in identifying useful subsets of samples to annotate from an unlabeled pool, but its high computational cost remains a barrier to its widespread applicability in the context of LLMs. To mitigate the annotation cost of SFT and circumvent the computational bottlenecks of active learning, we propose using experimental design. Experimental design techniques select the most informative samples to label, and typically maximize some notion of uncertainty and/or diversity. In our work, we implement a framework that evaluates several existing and novel experimental design techniques and find that these methods consistently yield significant gains in label efficiency with little computational overhead. On generative tasks, our methods achieve the same generalization performance with only $50\%$ of annotation cost required by random sampling.

apricot: Submodular selection for data summarization in Python

We present apricot, an open source Python package for selecting representative subsets from large data sets using submodular optimization. The package implements an efficient greedy selection algorithm that offers strong theoretical guarantees on the quality of the selected set. Two submodular set functions are implemented in apricot: facility location, which is broadly applicable but requires memory quadratic in the number of examples in the data set, and a feature-based function that is less broadly applicable but can scale to millions of examples. Apricot is extremely efficient, using both algorithmic speedups such as the lazy greedy algorithm and code optimizers such as numba. We demonstrate the use of subset selection by training machine learning models to comparable accuracy using either the full data set or a representative subset thereof. This paper presents an explanation of submodular selection, an overview of the features in apricot, and an application to several data sets. The code and tutorial Jupyter notebooks are available at https://github.com/jmschrei/apricot

Efficient Distributed Semi-Supervised Learning using Stochastic Regularization over Affinity Graphs

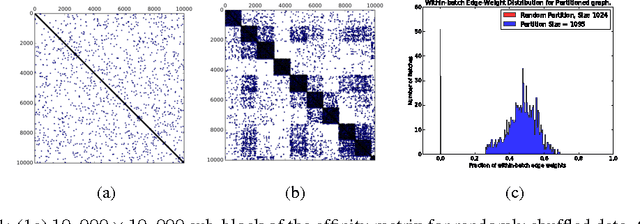
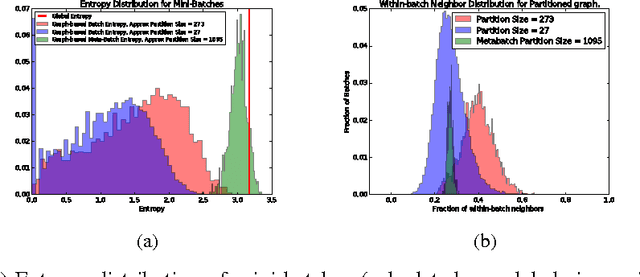
We describe a computationally efficient, stochastic graph-regularization technique that can be utilized for the semi-supervised training of deep neural networks in a parallel or distributed setting. We utilize a technique, first described in [13] for the construction of mini-batches for stochastic gradient descent (SGD) based on synthesized partitions of an affinity graph that are consistent with the graph structure, but also preserve enough stochasticity for convergence of SGD to good local minima. We show how our technique allows a graph-based semi-supervised loss function to be decomposed into a sum over objectives, facilitating data parallelism for scalable training of machine learning models. Empirical results indicate that our method significantly improves classification accuracy compared to the fully-supervised case when the fraction of labeled data is low, and in the parallel case, achieves significant speed-up in terms of wall-clock time to convergence. We show the results for both sequential and distributed-memory semi-supervised DNN training on a speech corpus.

Semi-Supervised Phone Classification using Deep Neural Networks and Stochastic Graph-Based Entropic Regularization

We describe a graph-based semi-supervised learning framework in the context of deep neural networks that uses a graph-based entropic regularizer to favor smooth solutions over a graph induced by the data. The main contribution of this work is a computationally efficient, stochastic graph-regularization technique that uses mini-batches that are consistent with the graph structure, but also provides enough stochasticity (in terms of mini-batch data diversity) for convergence of stochastic gradient descent methods to good solutions. For this work, we focus on results of frame-level phone classification accuracy on the TIMIT speech corpus but our method is general and scalable to much larger data sets. Results indicate that our method significantly improves classification accuracy compared to the fully-supervised case when the fraction of labeled data is low, and it is competitive with other methods in the fully labeled case.

Deep Submodular Functions

We start with an overview of a class of submodular functions called SCMMs (sums of concave composed with non-negative modular functions plus a final arbitrary modular). We then define a new class of submodular functions we call {\em deep submodular functions} or DSFs. We show that DSFs are a flexible parametric family of submodular functions that share many of the properties and advantages of deep neural networks (DNNs). DSFs can be motivated by considering a hierarchy of descriptive concepts over ground elements and where one wishes to allow submodular interaction throughout this hierarchy. Results in this paper show that DSFs constitute a strictly larger class of submodular functions than SCMMs. We show that, for any integer $k>0$, there are $k$-layer DSFs that cannot be represented by a $k'$-layer DSF for any $k'<k$. This implies that, like DNNs, there is a utility to depth, but unlike DNNs, the family of DSFs strictly increase with depth. Despite this, we show (using a "backpropagation" like method) that DSFs, even with arbitrarily large $k$, do not comprise all submodular functions. In offering the above results, we also define the notion of an antitone superdifferential of a concave function and show how this relates to submodular functions (in general), DSFs (in particular), negative second-order partial derivatives, continuous submodularity, and concave extensions. To further motivate our analysis, we provide various special case results from matroid theory, comparing DSFs with forms of matroid rank, in particular the laminar matroid. Lastly, we discuss strategies to learn DSFs, and define the classes of deep supermodular functions, deep difference of submodular functions, and deep multivariate submodular functions, and discuss where these can be useful in applications.