Efficient Distributed Semi-Supervised Learning using Stochastic Regularization over Affinity Graphs
Paper and Code
May 30, 2018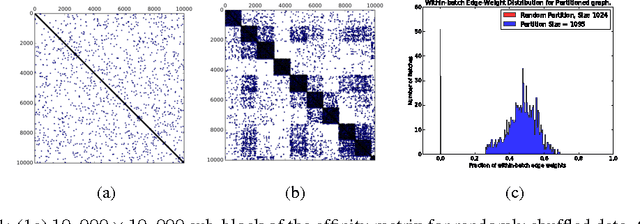
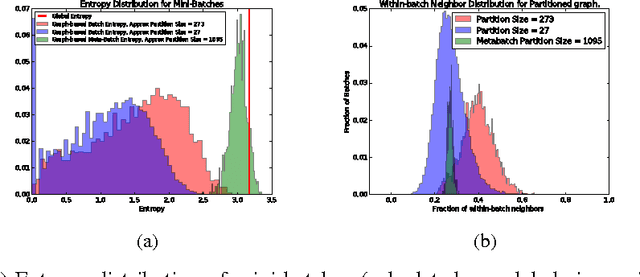

We describe a computationally efficient, stochastic graph-regularization technique that can be utilized for the semi-supervised training of deep neural networks in a parallel or distributed setting. We utilize a technique, first described in [13] for the construction of mini-batches for stochastic gradient descent (SGD) based on synthesized partitions of an affinity graph that are consistent with the graph structure, but also preserve enough stochasticity for convergence of SGD to good local minima. We show how our technique allows a graph-based semi-supervised loss function to be decomposed into a sum over objectives, facilitating data parallelism for scalable training of machine learning models. Empirical results indicate that our method significantly improves classification accuracy compared to the fully-supervised case when the fraction of labeled data is low, and in the parallel case, achieves significant speed-up in terms of wall-clock time to convergence. We show the results for both sequential and distributed-memory semi-supervised DNN training on a speech corpus.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge