Efficient Sparse PCA via Block-Diagonalization

Sparse Principal Component Analysis (Sparse PCA) is a pivotal tool in data analysis and dimensionality reduction. However, Sparse PCA is a challenging problem in both theory and practice: it is known to be NP-hard and current exact methods generally require exponential runtime. In this paper, we propose a novel framework to efficiently approximate Sparse PCA by (i) approximating the general input covariance matrix with a re-sorted block-diagonal matrix, (ii) solving the Sparse PCA sub-problem in each block, and (iii) reconstructing the solution to the original problem. Our framework is simple and powerful: it can leverage any off-the-shelf Sparse PCA algorithm and achieve significant computational speedups, with a minor additive error that is linear in the approximation error of the block-diagonal matrix. Suppose $g(k, d)$ is the runtime of an algorithm (approximately) solving Sparse PCA in dimension $d$ and with sparsity value $k$. Our framework, when integrated with this algorithm, reduces the runtime to $\mathcal{O}\left(\frac{d}{d^\star} \cdot g(k, d^\star) + d^2\right)$, where $d^\star \leq d$ is the largest block size of the block-diagonal matrix. For instance, integrating our framework with the Branch-and-Bound algorithm reduces the complexity from $g(k, d) = \mathcal{O}(k^3\cdot d^k)$ to $\mathcal{O}(k^3\cdot d \cdot (d^\star)^{k-1})$, demonstrating exponential speedups if $d^\star$ is small. We perform large-scale evaluations on many real-world datasets: for exact Sparse PCA algorithm, our method achieves an average speedup factor of 93.77, while maintaining an average approximation error of 2.15%; for approximate Sparse PCA algorithm, our method achieves an average speedup factor of 6.77 and an average approximation error of merely 0.37%.

Clustering with Queries under Semi-Random Noise

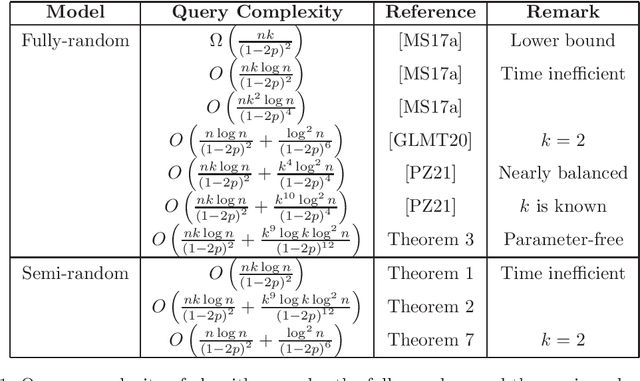
The seminal paper by Mazumdar and Saha \cite{MS17a} introduced an extensive line of work on clustering with noisy queries. Yet, despite significant progress on the problem, the proposed methods depend crucially on knowing the exact probabilities of errors of the underlying fully-random oracle. In this work, we develop robust learning methods that tolerate general semi-random noise obtaining qualitatively the same guarantees as the best possible methods in the fully-random model. More specifically, given a set of $n$ points with an unknown underlying partition, we are allowed to query pairs of points $u,v$ to check if they are in the same cluster, but with probability $p$, the answer may be adversarially chosen. We show that information theoretically $O\left(\frac{nk \log n} {(1-2p)^2}\right)$ queries suffice to learn any cluster of sufficiently large size. Our main result is a computationally efficient algorithm that can identify large clusters with $O\left(\frac{nk \log n} {(1-2p)^2}\right) + \text{poly}\left(\log n, k, \frac{1}{1-2p} \right)$ queries, matching the guarantees of the best known algorithms in the fully-random model. As a corollary of our approach, we develop the first parameter-free algorithm for the fully-random model, answering an open question by \cite{MS17a}.

Sparse PCA on fixed-rank matrices

Sparse PCA is the optimization problem obtained from PCA by adding a sparsity constraint on the principal components. Sparse PCA is NP-hard and hard to approximate even in the single-component case. In this paper we settle the computational complexity of sparse PCA with respect to the rank of the covariance matrix. We show that, if the rank of the covariance matrix is a fixed value, then there is an algorithm that solves sparse PCA to global optimality, whose running time is polynomial in the number of features. We also prove a similar result for the version of sparse PCA which requires the principal components to have disjoint supports.