Mingchen Ma
Learning Intersections of Two Margin Halfspaces under Factorizable Distributions
Nov 16, 2025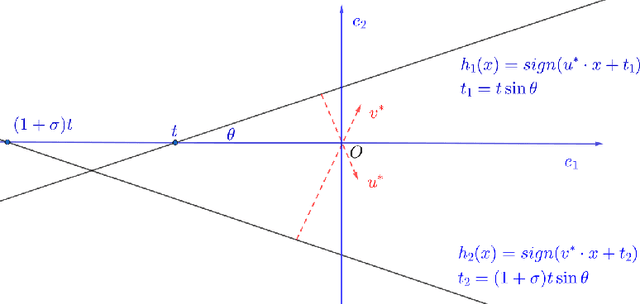
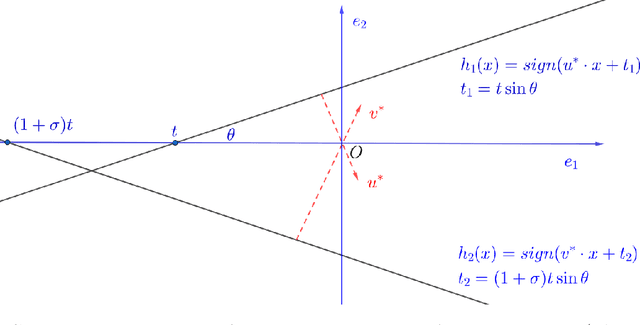
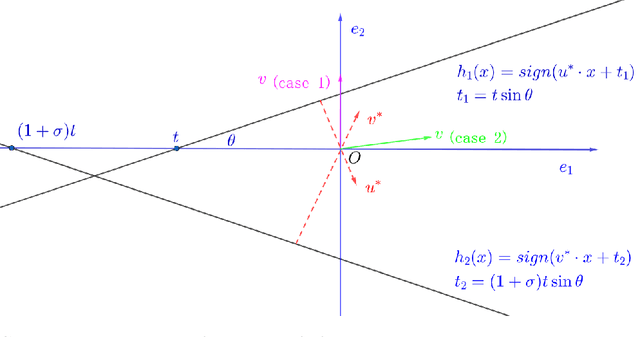

Abstract:Learning intersections of halfspaces is a central problem in Computational Learning Theory. Even for just two halfspaces, it remains a major open question whether learning is possible in polynomial time with respect to the margin $γ$ of the data points and their dimensionality $d$. The best-known algorithms run in quasi-polynomial time $d^{O(\log(1/γ))}$, and it has been shown that this complexity is unavoidable for any algorithm relying solely on correlational statistical queries (CSQ). In this work, we introduce a novel algorithm that provably circumvents the CSQ hardness barrier. Our approach applies to a broad class of distributions satisfying a natural, previously studied, factorizability assumption. Factorizable distributions lie between distribution-specific and distribution-free settings, and significantly extend previously known tractable cases. Under these distributions, we show that CSQ-based methods still require quasipolynomial time even for weakly learning, whereas our algorithm achieves $poly(d,1/γ)$ time by leveraging more general statistical queries (SQ), establishing a strong separation between CSQ and SQ for this simple realizable PAC learning problem. Our result is grounded in a rigorous analysis utilizing a novel duality framework that characterizes the moment tensor structure induced by the marginal distributions. Building on these structural insights, we propose new, efficient learning algorithms. These algorithms combine a refined variant of Jennrich's Algorithm with PCA over random projections of the moment tensor, along with a gradient-descent-based non-convex optimization framework.
Statistical Query Hardness of Multiclass Linear Classification with Random Classification Noise
Feb 17, 2025

Abstract:We study the task of Multiclass Linear Classification (MLC) in the distribution-free PAC model with Random Classification Noise (RCN). Specifically, the learner is given a set of labeled examples $(x, y)$, where $x$ is drawn from an unknown distribution on $R^d$ and the labels are generated by a multiclass linear classifier corrupted with RCN. That is, the label $y$ is flipped from $i$ to $j$ with probability $H_{ij}$ according to a known noise matrix $H$ with non-negative separation $\sigma: = \min_{i \neq j} H_{ii}-H_{ij}$. The goal is to compute a hypothesis with small 0-1 error. For the special case of two labels, prior work has given polynomial-time algorithms achieving the optimal error. Surprisingly, little is known about the complexity of this task even for three labels. As our main contribution, we show that the complexity of MLC with RCN becomes drastically different in the presence of three or more labels. Specifically, we prove super-polynomial Statistical Query (SQ) lower bounds for this problem. In more detail, even for three labels and constant separation, we give a super-polynomial lower bound on the complexity of any SQ algorithm achieving optimal error. For a larger number of labels and smaller separation, we show a super-polynomial SQ lower bound even for the weaker goal of achieving any constant factor approximation to the optimal loss or even beating the trivial hypothesis.
AutoCBT: An Autonomous Multi-agent Framework for Cognitive Behavioral Therapy in Psychological Counseling
Jan 16, 2025



Abstract:Traditional in-person psychological counseling remains primarily niche, often chosen by individuals with psychological issues, while online automated counseling offers a potential solution for those hesitant to seek help due to feelings of shame. Cognitive Behavioral Therapy (CBT) is an essential and widely used approach in psychological counseling. The advent of large language models (LLMs) and agent technology enables automatic CBT diagnosis and treatment. However, current LLM-based CBT systems use agents with a fixed structure, limiting their self-optimization capabilities, or providing hollow, unhelpful suggestions due to redundant response patterns. In this work, we utilize Quora-like and YiXinLi single-round consultation models to build a general agent framework that generates high-quality responses for single-turn psychological consultation scenarios. We use a bilingual dataset to evaluate the quality of single-response consultations generated by each framework. Then, we incorporate dynamic routing and supervisory mechanisms inspired by real psychological counseling to construct a CBT-oriented autonomous multi-agent framework, demonstrating its general applicability. Experimental results indicate that AutoCBT can provide higher-quality automated psychological counseling services.
Active Learning of General Halfspaces: Label Queries vs Membership Queries
Dec 31, 2024Abstract:We study the problem of learning general (i.e., not necessarily homogeneous) halfspaces under the Gaussian distribution on $R^d$ in the presence of some form of query access. In the classical pool-based active learning model, where the algorithm is allowed to make adaptive label queries to previously sampled points, we establish a strong information-theoretic lower bound ruling out non-trivial improvements over the passive setting. Specifically, we show that any active learner requires label complexity of $\tilde{\Omega}(d/(\log(m)\epsilon))$, where $m$ is the number of unlabeled examples. Specifically, to beat the passive label complexity of $\tilde{O} (d/\epsilon)$, an active learner requires a pool of $2^{poly(d)}$ unlabeled samples. On the positive side, we show that this lower bound can be circumvented with membership query access, even in the agnostic model. Specifically, we give a computationally efficient learner with query complexity of $\tilde{O}(\min\{1/p, 1/\epsilon\} + d\cdot polylog(1/\epsilon))$ achieving error guarantee of $O(opt)+\epsilon$. Here $p \in [0, 1/2]$ is the bias and $opt$ is the 0-1 loss of the optimal halfspace. As a corollary, we obtain a strong separation between the active and membership query models. Taken together, our results characterize the complexity of learning general halfspaces under Gaussian marginals in these models.
Active Learning with Simple Questions
May 13, 2024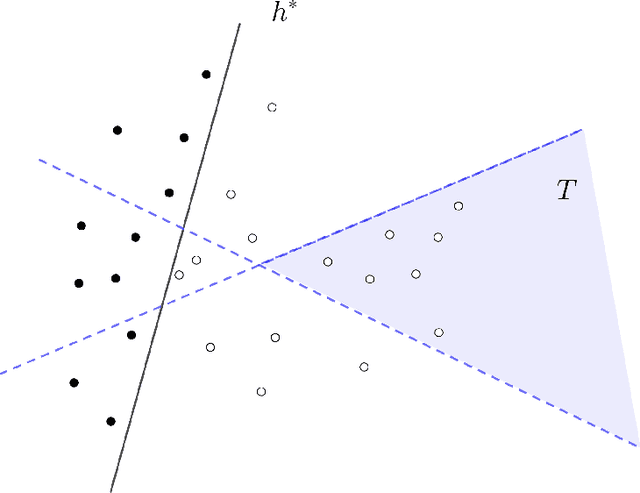

Abstract:We consider an active learning setting where a learner is presented with a pool S of n unlabeled examples belonging to a domain X and asks queries to find the underlying labeling that agrees with a target concept h^* \in H. In contrast to traditional active learning that queries a single example for its label, we study more general region queries that allow the learner to pick a subset of the domain T \subset X and a target label y and ask a labeler whether h^*(x) = y for every example in the set T \cap S. Such more powerful queries allow us to bypass the limitations of traditional active learning and use significantly fewer rounds of interactions to learn but can potentially lead to a significantly more complex query language. Our main contribution is quantifying the trade-off between the number of queries and the complexity of the query language used by the learner. We measure the complexity of the region queries via the VC dimension of the family of regions. We show that given any hypothesis class H with VC dimension d, one can design a region query family Q with VC dimension O(d) such that for every set of n examples S \subset X and every h^* \in H, a learner can submit O(d log n) queries from Q to a labeler and perfectly label S. We show a matching lower bound by designing a hypothesis class H with VC dimension d and a dataset S \subset X of size n such that any learning algorithm using any query class with VC dimension O(d) must make poly(n) queries to label S perfectly. Finally, we focus on well-studied hypothesis classes including unions of intervals, high-dimensional boxes, and d-dimensional halfspaces, and obtain stronger results. In particular, we design learning algorithms that (i) are computationally efficient and (ii) work even when the queries are not answered based on the learner's pool of examples S but on some unknown superset L of S
Buying Information for Stochastic Optimization
Jun 06, 2023Abstract:Stochastic optimization is one of the central problems in Machine Learning and Theoretical Computer Science. In the standard model, the algorithm is given a fixed distribution known in advance. In practice though, one may acquire at a cost extra information to make better decisions. In this paper, we study how to buy information for stochastic optimization and formulate this question as an online learning problem. Assuming the learner has an oracle for the original optimization problem, we design a $2$-competitive deterministic algorithm and a $e/(e-1)$-competitive randomized algorithm for buying information. We show that this ratio is tight as the problem is equivalent to a robust generalization of the ski-rental problem, which we call super-martingale stopping. We also consider an adaptive setting where the learner can choose to buy information after taking some actions for the underlying optimization problem. We focus on the classic optimization problem, Min-Sum Set Cover, where the goal is to quickly find an action that covers a given request drawn from a known distribution. We provide an $8$-competitive algorithm running in polynomial time that chooses actions and decides when to buy information about the underlying request.
Clustering with Queries under Semi-Random Noise
Jun 15, 2022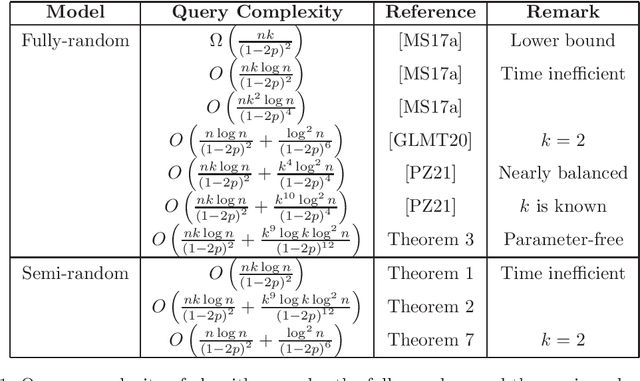
Abstract:The seminal paper by Mazumdar and Saha \cite{MS17a} introduced an extensive line of work on clustering with noisy queries. Yet, despite significant progress on the problem, the proposed methods depend crucially on knowing the exact probabilities of errors of the underlying fully-random oracle. In this work, we develop robust learning methods that tolerate general semi-random noise obtaining qualitatively the same guarantees as the best possible methods in the fully-random model. More specifically, given a set of $n$ points with an unknown underlying partition, we are allowed to query pairs of points $u,v$ to check if they are in the same cluster, but with probability $p$, the answer may be adversarially chosen. We show that information theoretically $O\left(\frac{nk \log n} {(1-2p)^2}\right)$ queries suffice to learn any cluster of sufficiently large size. Our main result is a computationally efficient algorithm that can identify large clusters with $O\left(\frac{nk \log n} {(1-2p)^2}\right) + \text{poly}\left(\log n, k, \frac{1}{1-2p} \right)$ queries, matching the guarantees of the best known algorithms in the fully-random model. As a corollary of our approach, we develop the first parameter-free algorithm for the fully-random model, answering an open question by \cite{MS17a}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge