The Internet of Federated Things : A Vision for the Future and In-depth Survey of Data-driven Approaches for Federated Learning

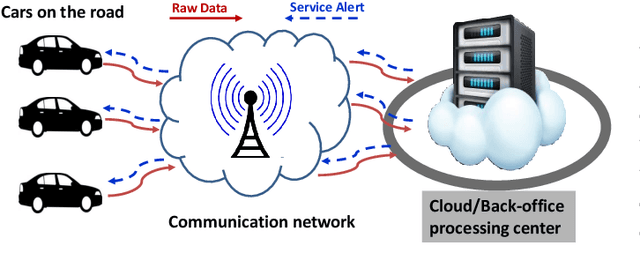
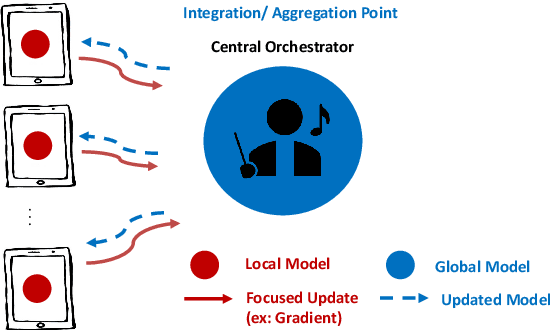
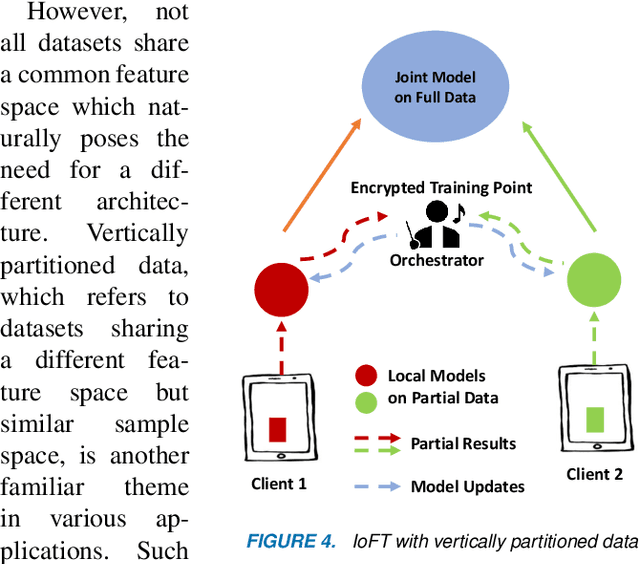
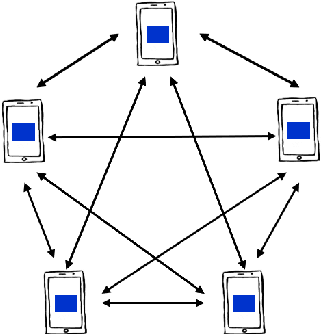
The Internet of Things (IoT) is on the verge of a major paradigm shift. In the IoT system of the future, IoFT, the cloud will be substituted by the crowd where model training is brought to the edge, allowing IoT devices to collaboratively extract knowledge and build smart analytics/models while keeping their personal data stored locally. This paradigm shift was set into motion by the tremendous increase in computational power on IoT devices and the recent advances in decentralized and privacy-preserving model training, coined as federated learning (FL). This article provides a vision for IoFT and a systematic overview of current efforts towards realizing this vision. Specifically, we first introduce the defining characteristics of IoFT and discuss FL data-driven approaches, opportunities, and challenges that allow decentralized inference within three dimensions: (i) a global model that maximizes utility across all IoT devices, (ii) a personalized model that borrows strengths across all devices yet retains its own model, (iii) a meta-learning model that quickly adapts to new devices or learning tasks. We end by describing the vision and challenges of IoFT in reshaping different industries through the lens of domain experts. Those industries include manufacturing, transportation, energy, healthcare, quality & reliability, business, and computing.

On Negative Transfer and Structure of Latent Functions in Multi-output Gaussian Processes

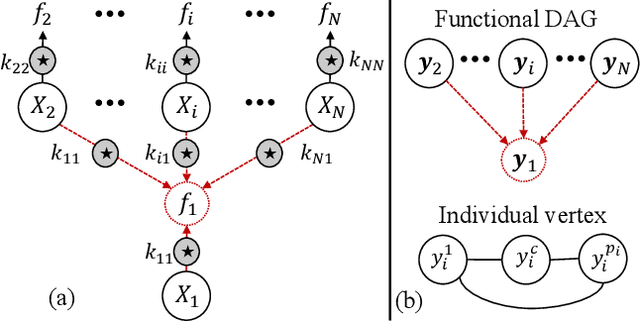
The multi-output Gaussian process ($\mathcal{MGP}$) is based on the assumption that outputs share commonalities, however, if this assumption does not hold negative transfer will lead to decreased performance relative to learning outputs independently or in subsets. In this article, we first define negative transfer in the context of an $\mathcal{MGP}$ and then derive necessary conditions for an $\mathcal{MGP}$ model to avoid negative transfer. Specifically, under the convolution construction, we show that avoiding negative transfer is mainly dependent on having a sufficient number of latent functions $Q$ regardless of the flexibility of the kernel or inference procedure used. However, a slight increase in $Q$ leads to a large increase in the number of parameters to be estimated. To this end, we propose two latent structures that scale to arbitrarily large datasets, can avoid negative transfer and allow any kernel or sparse approximations to be used within. These structures also allow regularization which can provide consistent and automatic selection of related outputs.

The Rényi Gaussian Process

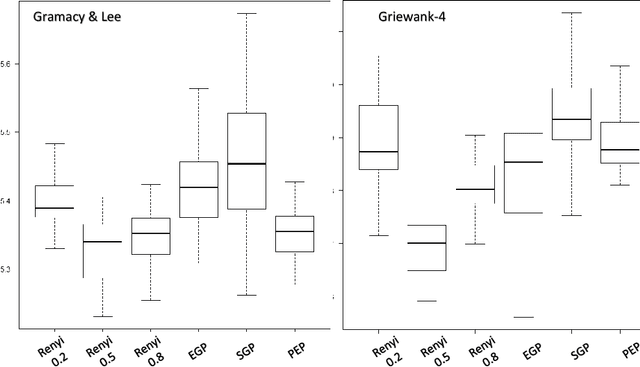
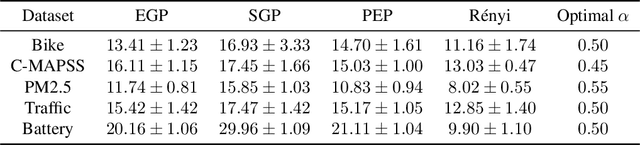
In this article we introduce an alternative closed form lower bound on the Gaussian process ($\mathcal{GP}$) likelihood based on the R\'enyi $\alpha$-divergence. This new lower bound can be viewed as a convex combination of the Nystr\"om approximation and the exact $\mathcal{GP}$. The key advantage of this bound, is its capability to control and tune the enforced regularization on the model and thus is a generalization of the traditional sparse variational $\mathcal{GP}$ regression. From the theoretical perspective, we show that with probability at least $1-\delta$, the R\'enyi $\alpha$-divergence between the variational distribution and the true posterior becomes arbitrarily small as the number of data points increase.

Minimizing Negative Transfer of Knowledge in Multivariate Gaussian Processes: A Scalable and Regularized Approach

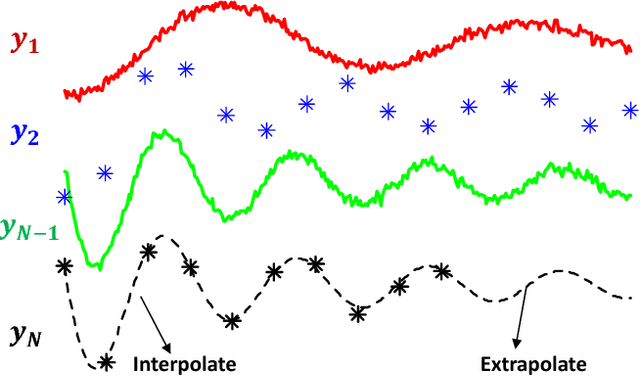
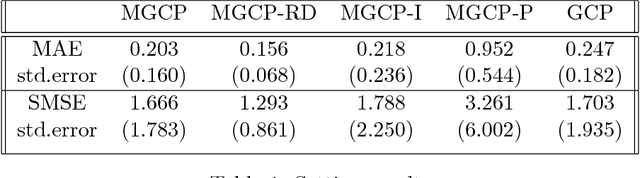
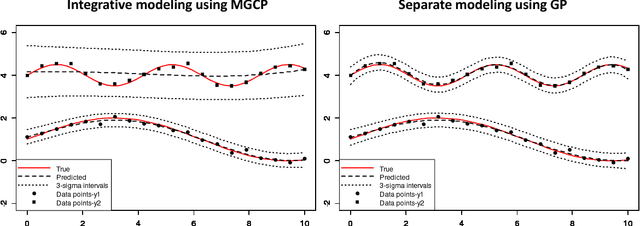
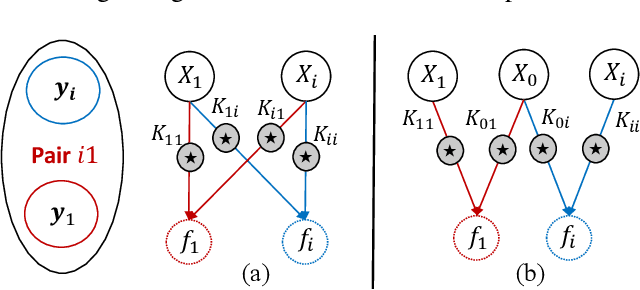
Recently there has been an increasing interest in the multivariate Gaussian process (MGP) which extends the Gaussian process (GP) to deal with multiple outputs. One approach to construct the MGP and account for non-trivial commonalities amongst outputs employs a convolution process (CP). The CP is based on the idea of sharing latent functions across several convolutions. Despite the elegance of the CP construction, it provides new challenges that need yet to be tackled. First, even with a moderate number of outputs, model building is extremely prohibitive due to the huge increase in computational demands and number of parameters to be estimated. Second, the negative transfer of knowledge may occur when some outputs do not share commonalities. In this paper we address these issues. We propose a regularized pairwise modeling approach for the MGP established using CP. The key feature of our approach is to distribute the estimation of the full multivariate model into a group of bivariate GPs which are individually built. Interestingly pairwise modeling turns out to possess unique characteristics, which allows us to tackle the challenge of negative transfer through penalizing the latent function that facilitates information sharing in each bivariate model. Predictions are then made through combining predictions from the bivariate models within a Bayesian framework. The proposed method has excellent scalability when the number of outputs is large and minimizes the negative transfer of knowledge between uncorrelated outputs. Statistical guarantees for the proposed method are studied and its advantageous features are demonstrated through numerical studies.

Functional Principal Component Analysis for Extrapolating Multi-stream Longitudinal Data

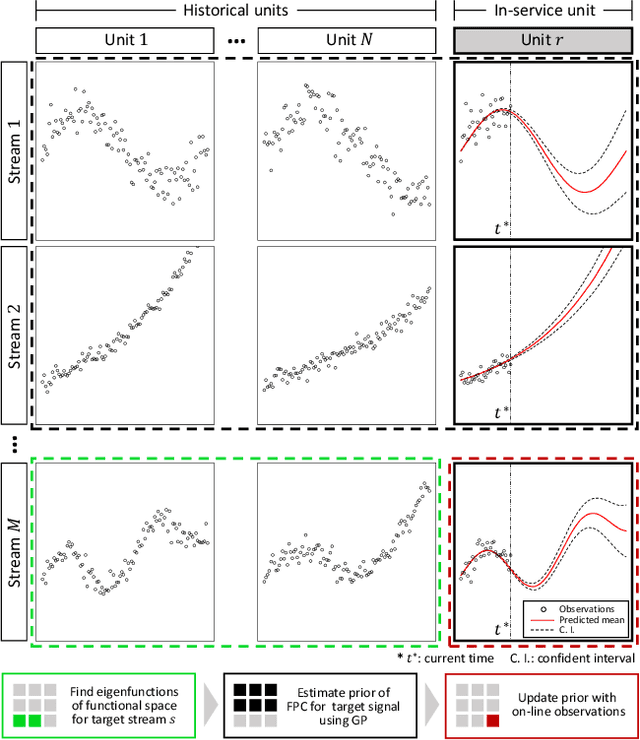
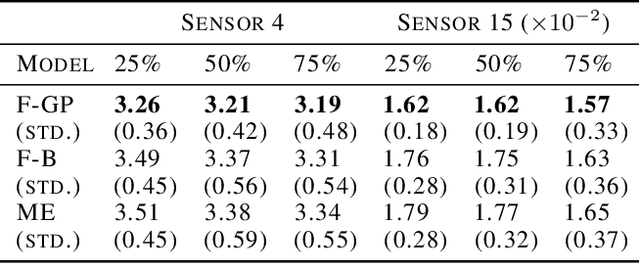
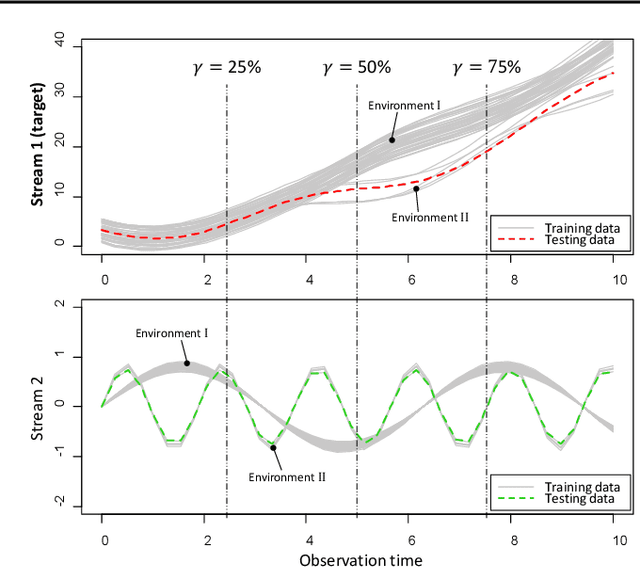
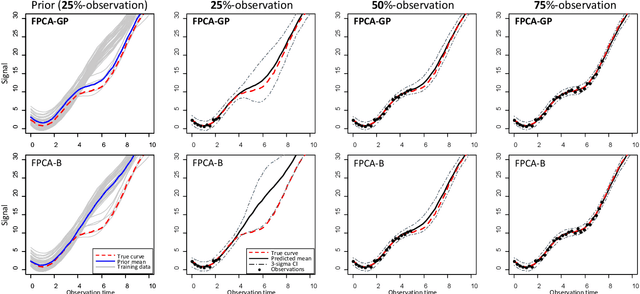
The advance of modern sensor technologies enables collection of multi-stream longitudinal data where multiple signals from different units are collected in real-time. In this article, we present a non-parametric approach to predict the evolution of multi-stream longitudinal data for an in-service unit through borrowing strength from other historical units. Our approach first decomposes each stream into a linear combination of eigenfunctions and their corresponding functional principal component (FPC) scores. A Gaussian process prior for the FPC scores is then established based on a functional semi-metric that measures similarities between streams of historical units and the in-service unit. Finally, an empirical Bayesian updating strategy is derived to update the established prior using real-time stream data obtained from the in-service unit. Experiments on synthetic and real world data show that the proposed framework outperforms state-of-the-art approaches and can effectively account for heterogeneity as well as achieve high predictive accuracy.

Variational Inference of Joint Models using Multivariate Gaussian Convolution Processes

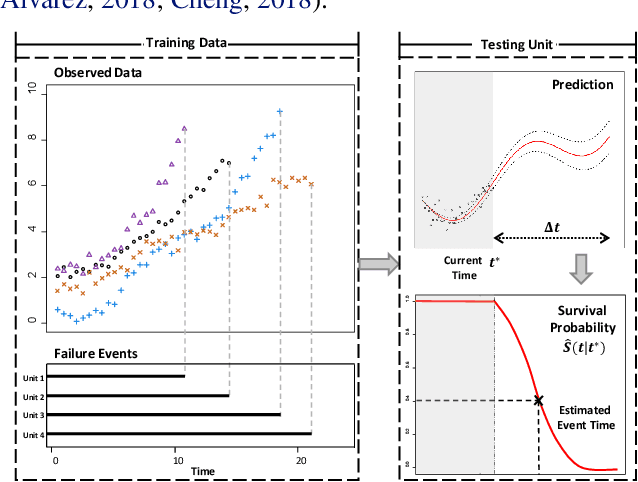
We present a non-parametric prognostic framework for individualized event prediction based on joint modeling of both longitudinal and time-to-event data. Our approach exploits a multivariate Gaussian convolution process (MGCP) to model the evolution of longitudinal signals and a Cox model to map time-to-event data with longitudinal data modeled through the MGCP. Taking advantage of the unique structure imposed by convolved processes, we provide a variational inference framework to simultaneously estimate parameters in the joint MGCP-Cox model. This significantly reduces computational complexity and safeguards against model overfitting. Experiments on synthetic and real world data show that the proposed framework outperforms state-of-the art approaches built on two-stage inference and strong parametric assumptions.