On Negative Transfer and Structure of Latent Functions in Multi-output Gaussian Processes
Paper and Code
Apr 06, 2020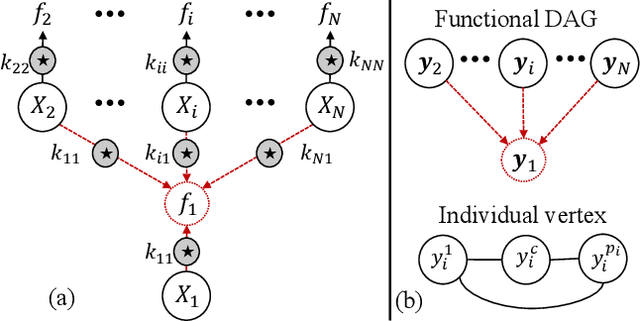

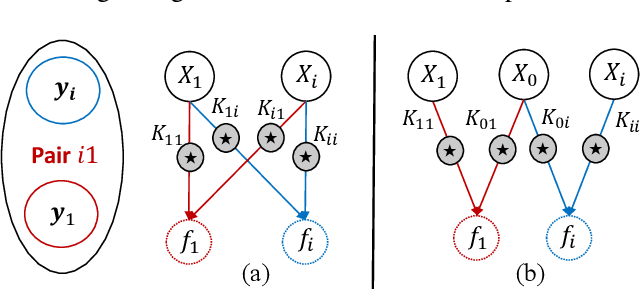

The multi-output Gaussian process ($\mathcal{MGP}$) is based on the assumption that outputs share commonalities, however, if this assumption does not hold negative transfer will lead to decreased performance relative to learning outputs independently or in subsets. In this article, we first define negative transfer in the context of an $\mathcal{MGP}$ and then derive necessary conditions for an $\mathcal{MGP}$ model to avoid negative transfer. Specifically, under the convolution construction, we show that avoiding negative transfer is mainly dependent on having a sufficient number of latent functions $Q$ regardless of the flexibility of the kernel or inference procedure used. However, a slight increase in $Q$ leads to a large increase in the number of parameters to be estimated. To this end, we propose two latent structures that scale to arbitrarily large datasets, can avoid negative transfer and allow any kernel or sparse approximations to be used within. These structures also allow regularization which can provide consistent and automatic selection of related outputs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge